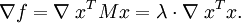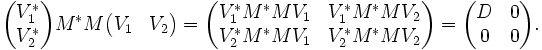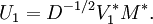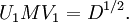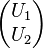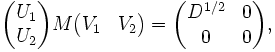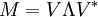Décomposition en valeurs singulières - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, le procédé d'algèbre linéaire de décomposition en valeurs singulières (ou SVD, de l'anglais : Singular Value Decomposition) d'une matrice est un outil important de factorisation des matrices rectangulaires réelles ou complexes. Ses applications s'étendent du traitement du signal aux statistiques, en passant par la météorologie.
Le théorème spectral énonce qu'une matrice normale peut être diagonalisée par une base orthonormée de vecteurs propres. On peut voir cette décomposition comme une généralisation du théorème spectral à des matrices arbitraires, qui ne sont pas nécessairement carrées.
Contexte mathématique
Énoncé du théorème
Soit M une matrice m×n dont les coefficients appartiennent au corps K, où K = R ou K = C. Alors il existe une factorisation de la forme :
-
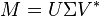
avec U une matrice unitaire m×m sur K, Σ une matrice m×n dont les coefficients diagonaux sont des réels positifs ou nuls et tous les autres sont nuls (c'est donc une matrice diagonale dont on impose que les coefficients soient positifs ou nuls), et V* est la matrice adjointe à V, matrice unitaire n×n sur K. On appelle cette factorisation la décomposition en valeurs singulières de M.
- La matrice V contient un ensemble de vecteurs de base orthonormés pour M, dits « d'entrée » ou « d'analyse » ;
- La matrice U contient un ensemble de vecteurs de base orthonormés pour M, dits « de sortie » ;
- La matrice Σ contient les valeurs singulières de la matrice M.
Une convention courante est de ranger les valeurs Σi,i par ordre décroissant. Alors, la matrice diagonale Σ est déterminée de façon unique par M (mais U et V ne le sont pas).
Existence
Une valeur propre λ d'une matrice est caractérisée par la relation M u = λ u. Quand M est hermitienne, une autre caractérisation différente est envisageable. Soit M une matrice n × n symétrique réelle. On pose f: Rn → R telle que f(x) = xT M x. Cette fonction est continue et atteint son maximum en un certain vecteur u quand elle est restreinte à la boule unité fermée {||x|| ≤ 1}. D'après le théorème des multiplicateurs de Lagrange, u vérifie :
On montre facilement que la relation ci-dessus donne M u = λ u. Ainsi, λ est la plus grande valeur propre de M. Les mêmes opérations sur le complément orthogonal de u donne la seconde plus grande valeur, et ainsi de suite. Le cas d'une matrice complexe hermitienne est similaire, avec f(x) = x* M x une fonction de 2n variables à valeurs réelles.
Les valeurs singulières sont similaires, en tant qu'elles peuvent être décrites de façon algébrique ou à partir de principes variationnels. En revanche, au contraire du cas des valeurs propres, l'hermiticité et la symétrie de M ne sont plus nécessaires.
Preuve utilisant l'algèbre
Soit M une matrice complexe m×n. Alors M*M est positive semi-définie, donc hermitienne. D'après le théorème spectral, il existe une matrice unitaire carrée de côté n, notée V, telle que :
-
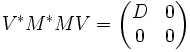
où D est diagonale et définie positive. En écrivant V de façon appropriée :
Ainsi, V*1M*MV1 = D, et MV2 = 0. On pose :
Alors on a :
On constate que c'est presque le résultat attendu, à ceci près que U1 et V1 ne sont pas unitaires dans le cas général. U1 est une isométrie partielle (U1U*1 = I ) alors que V1 est une isométrie (V*1V1 = I ). Pour achever la démonstration, on doit en quelque sorte « compléter » ces matrices pour les rendre unitaires.
V2 convient pour V1. De même, on peut choisir U2 tel que :
soit unitaire. Un calcul montre que :
ce qui correspond au résultat attendu.
On aurait également pu commencer la démonstration en diagonalisant MM* au lieu de M*M, on aurait alors montré directement que MM* et M*M ont même valeurs propres non-nulles.
Caractérisation alternative
Les valeurs singulières peuvent également être caractérisées comme maxima de uTMv, considérée comme une fonction de u et v, sur des sous-espaces particuliers. Les vecteurs singuliers sont les valeurs de u et v pour lesquelles ces maxima sont atteints.
Soit M une matrice réelle m × n. Soit Sm − 1 et Sn − 1 l'ensemble des vecteurs unitaires (selon la norme 2) de Rm et Rn respectivement. On pose la fonction :
-
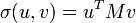
pour les vecteurs u ∈ Sm − 1 et v ∈ Sn − 1.
On considère la fonction σ restreinte à Sm − 1 × Sn − 1. Puisqu'à la fois Sm − 1 et Sn − 1 sont des ensembles compacts, leur produit est également compact. En outre, puisque σ est continue, elle atteint son maximum pour au moins une paire de vecteurs u ∈ Sm − 1 et v ∈ Sn − 1. Ce maximum est noté σ1, et les vecteurs correspondants sont notés u1 et v1. Puisque σ1 est la plus grande valeur de σ(u,v), elle est positive : si elle était négative, en changeant le signe de u1 ou de v1, on la rendrait positive - et donc plus grande.
Lemme — u1 et v1 sont respectivement vecteurs singuliers à gauche et à droite pour M associés à σ1.
Démonstration — De même que pour le cas des valeurs propres, en supposant que les deux vecteurs vérifient l'équation de Lagrange :
-
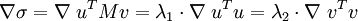
On montre que cela donne :
- Mv1 = 2λ1u1 + 0, et
- MTu1 = 0 + 2λ2v1.
En multipliant la première équation à gauche par
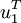
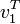
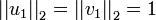
-
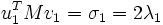
-
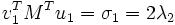
Ainsi, σ1 = 2 λ1 = 2 λ2. Par les propriétés de la fonction Φ définie par
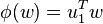
-
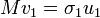
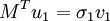
D'autres vecteurs singuliers et valeurs singulières peuvent être obtenus en maximisant σ(u, v) sur u, v, qui sont orthogonaux à u1 et v1, respectivement.
On peut de même traiter le cas de matrices complexes.
Valeurs singulières et vecteurs singuliers
Un réel positif σ est appelé valeur singulière de M si et seulement s'il existe un vecteur unitaire u dans Km et un vecteur unitaire v dans Kn tel que :
-
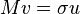
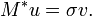
Les vecteurs u et v sont appelés vecteur singulier à gauche et vecteur singulier à droite pour σ, respectivement.
Dans toute décomposition en valeurs singulières,
-
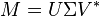
les coefficients diagonaux de Σ sont égaux aux valeurs singulières de M. Les colonnes de U et de V sont, respectivement, vecteur singulier à gauche et à droite pour les valeurs singulières correspondantes.
Par conséquent, le théorème ci-dessus énonce que :
- Une matrice M m × n possède au moins 1 et au plus p = min(m,n) valeurs singulières distinctes ;
- Il est toujours possible de trouver une base unitaire pour Km constituée des vecteurs singuliers à gauche de M ;
- Il est toujours possible de trouver une base unitaire pour Kn constituée des vecteurs singuliers à droite de M ;
Une valeur singulière pour laquelle on peut trouver deux vecteurs singuliers à gauche (respectivement, à droite) qui ne sont pas linéairements indépendants est dite dégénérée.
Les valeurs singulières non-dégénérées ont toujours un unique vecteur singulier à gauche et à droite, à un déphasage près, c’est-à-dire à une multiplication par un facteur de la forme eiφ près (pour des réels, à un signe près). Par conséquent, si toutes les valeurs singulières de M sont non-dégénérées et non-nulles, alors sa décomposition en valeurs singulières est unique, à une multiplication d'une colonne de U et de la colonne de V correspondante par un même de déphasage.
Les valeurs singulières dégénérées, par définition, possèdent plusieurs vecteurs singuliers. De plus, si u1 et u2 sont deux vecteurs singuliers à gauche qui correspondent à une même valeur singulière σ, alors tout vecteur unitaire obtenu par combinaison linéaire de ces deux vecteurs est également un vecteur singulier à gauche pour σ. Il en est de même pour les vecteurs singuliers à droites. Ainsi, si M possède des valeurs singulières dégénérées, alors sa décomposition en valeurs singulières n'est pas unique.
Lien avec la décomposition en valeurs propres
La décomposition en valeurs singulières est très générale, dans le sens où elle s'applique à toute matrice rectangulaire m × n. La décomposition en valeurs propres, en revanche, ne fonctionne que pour certaines matrices carrées. Néanmoins, quand elles sont toutes les deux définies, elles sont liées.
Dans le cas d'une matrice M hermitienne semi-définie positive, c'est-à-dire dont toutes les valeurs propres sont des réels positifs, alors les valeurs singulières et vecteurs singuliers correspondent aux valeurs propres et vecteurs propres de M :
Plus généralement, étant donnée une décomposition en valeurs singulières de M, alors on a :
-
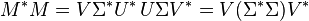
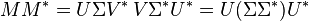
Le côté droit de ces relations décrit la décomposition en valeurs propres du côté gauche. Ainsi, le carré de la valeur absolue de chaque valeur singulière non-nulle de M est égal à la valeur absolue de la valeur propre non-nulle correspondante de M * M et de MM * . En outre, les colonnes de U (vecteurs singuliers à gauche) sont vecteurs propres pour MM * , et les colonnes de V (vecteurs singuliers à droite) sont vecteurs propres de M * M.
Interprétation géométrique
Puisque U et V sont unitaires, on sait que les colonnes u1,...,um de U forme une base orthonormée de Km et que les colonnes v1,...,vn de V forment une base orthonormée de Kn (par rapport au produit scalaire sur ces espaces).
La transformation linéaire T: Kn → Km, qui à chaque vecteur x associe Mx, a une expression relativement simple dans ces bases orthonormées : T(vi) = σi ui, pour i = 1,...,min(m,n), où σi est le i-ème coefficient diagonal de Σ, et T(vi) = 0 pour i > min(m,n).
Le contenu géométrique du théorème de décomposition en valeurs singulières peut être résumé ainsi : pour toute application linéaire T : Kn → Km, on peut trouver une base orthonormale pour Kn et une base orthonormale pour Km telles que T associe au i-ème vecteur de base de Kn un multiple positif du i-ème vecteur de base de Km, les vecteurs restants ayant pour image 0. Dans ces bases, l'application T est ainsi représentée par une matrice diagonale dont les coefficients sont des réels positifs.
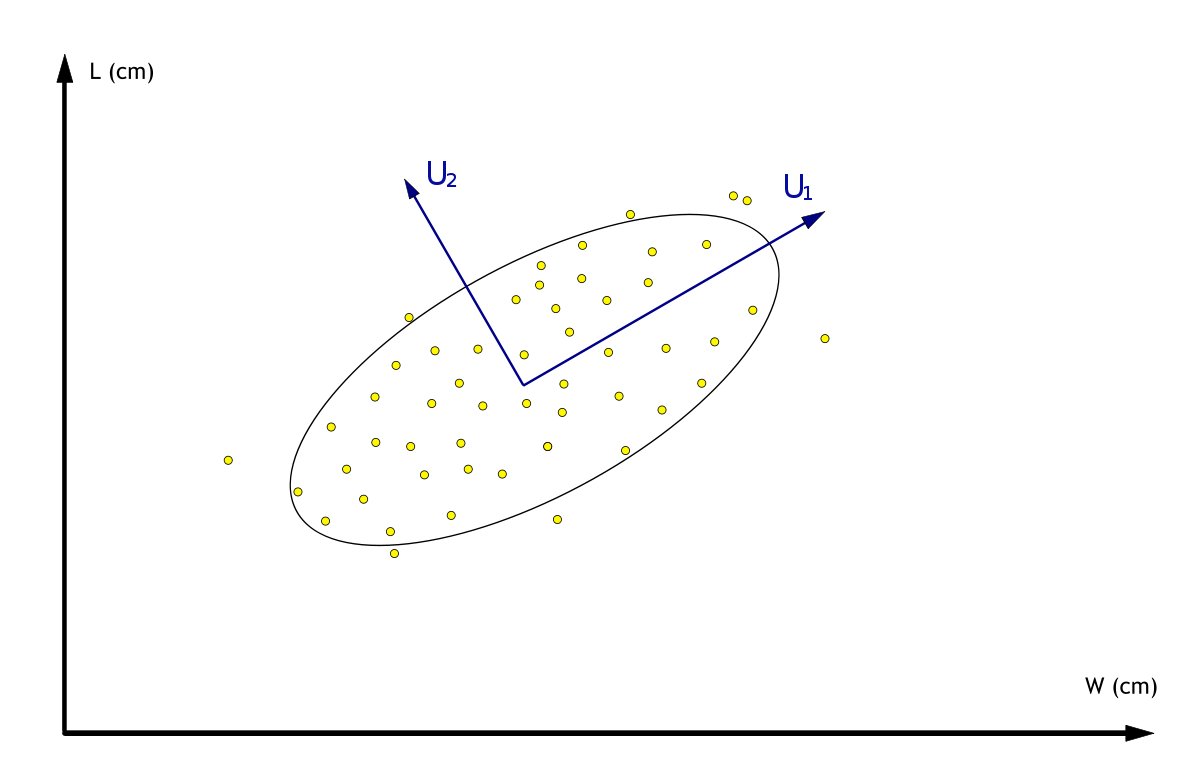
Interprétation statistique
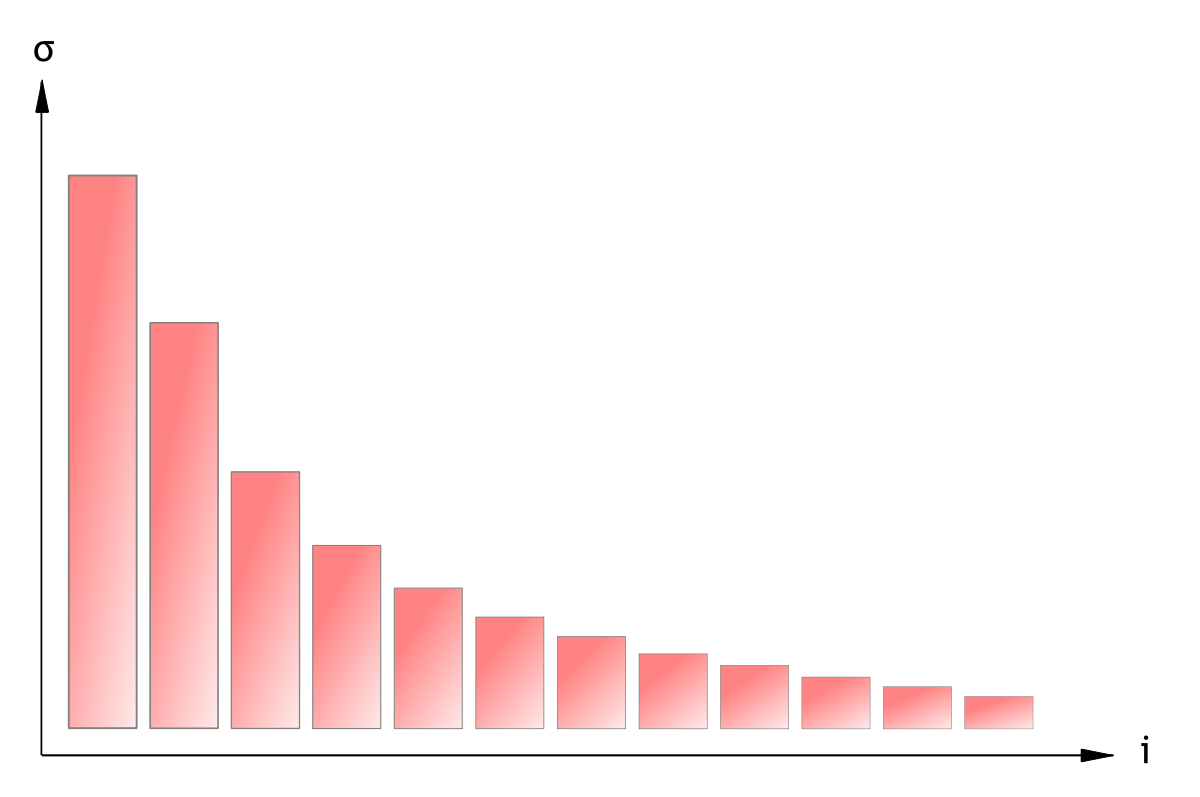
On peut également interpréter cette décomposition dans l'esprit de l'étude statistique d'un ensemble de données. Alors, les principales colonnes de U représentent les tendances de l'ensemble d'étude (les vecteurs de U représentent les « directions de plus grande variation » de l'ensemble). Les valeurs diagonales de Σ sont alors analogues à l' « énergie » ou la « représentativité » qui va pondérer ces comportements ; elles décroissent d'autant plus vite que l'ensemble statistique est ordonné.
On peut considérer, par exemple dans l'optique du data mining, que les informations « importantes » de l'ensemble sont celles qui présentent une structure plus marquée. Alors, en annulant la diagonale de Σ au-delà d'un certain indice, puis en reconstituant la matrice de départ, on obtient des données filtrées, représentant l'information dominante de l'ensemble de départ. De façon équivalente, on peut considérer nulles des données d'énergie inférieure à un certain seuil.
Ainsi, la SVD permet de construire un modèle empirique, sans théorie sous-jacente, d'autant plus précis qu'on y injecte de termes.
Il est par ailleurs possible de reconstruire, en utilisant une base de vecteurs singuliers d'un premier jeu de données, un autre jeu de données avec plus ou moins de précision, afin de déterminer la similarité entre les deux. Selon ce principe, des systèmes de décomposition, de reconnaissance et de reconstruction faciale ont été développés.
L'efficacité de la méthode dépend en particulier de la manière dont on lui présente les informations. Dans l'exemple d'un visage, si on utilise « bêtement » la luminosité des différents pixels d'une photographie pour construire une base de vecteurs singuliers, alors il sera difficile de reconstruire le même visage dans une pose légèrement différente (ou si l'éclairement du visage a varié) : les pixels ont changé - parfois beaucoup - mais pas l'information implicite (à savoir le visage). On préfère, dans ces domaines d'application, traiter les données dans l'espace, d'où l'ajout d'un système de reconnaissance en 3D, qui permet d'« expliquer » les variations observées en reliant celles-ci, et de les relier aux données connues.