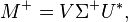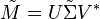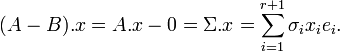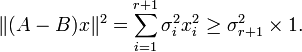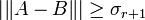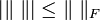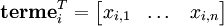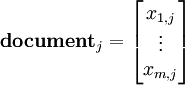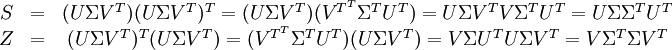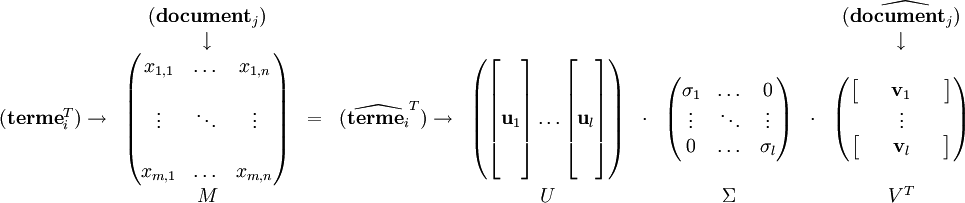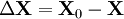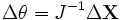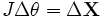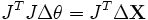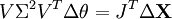Décomposition en valeurs singulières - Définition
La liste des auteurs de cet article est disponible ici.
Utilisations
Calcul du pseudo-inverse
La décomposition en valeurs singulières permet de calculer le pseudo-inverse d'une matrice. En effet, le pseudo-inverse d'une matrice M connaissant sa décomposition en valeurs singulières M = UΣV * , est donné par :
avec Σ+ la transposée de Σ où tout coefficient non-nul est remplacé par son inverse. Le pseudo-inverse lui-même permet de résoudre la méthode des moindres carrés.
Image, rang et noyau
Une autre utilisation de la décomposition en valeurs singulières est la représentation explicite de l'image et du noyau d'une matrice M. Les vecteurs singuliers à droite correspondant aux valeurs singulières nulles de M engendrent le noyau de M. Les vecteurs singuliers à gauche correspondant aux valeurs singulières non-nulles de M engendrent son image.
Par conséquent, le rang de M est égal au nombre de valeurs singulières non-nulles de M. De plus, les rangs de M, de M * M et de MM * sont égaux. M * M et MM * ont les mêmes valeurs propres non-nulles.
En algèbre linéaire, on peut prévoir numériquement le rang effectif d'une matrice, puisque les erreurs d'arrondi pourraient autrement engendrer des valeurs petites mais non-nulles, faussant le calcul du rang de la matrice.
Approximations de matrices, le théorème d'Eckart Young
Certaines applications pratiques ont besoin de résoudre un problème d'approximation de matrices M à partir d'une matrice
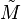
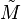
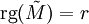
avec
On se limite aux matrices carrées par souci de simplification. On utilise le symbole norme triple pour représenter la norme spectrale. On prouve le théorème d'Eckart Young tout d'abord pour la norme spectrale. Sans perte de généralité, on peut supposer que A est une matrice diagonale et donc que U et V sont la matrice identité. On pose donc A = Σ. Les termes diagonaux de A sont notés σi. Ils sont triés par ordre décroissant. On a donc
On considère une matrice B quelconque de rang r. On considère le sous-espace vectoriel E de

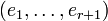
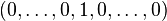
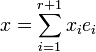
Comme les vecteurs ei sont orthogonaux et normés, on obtient:
Par définition de la norme spectrale, on déduit donc que quelle que soit la matrice B, on a
On conclut la preuve en choisissant
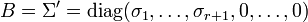
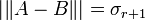
Donc B = Σ' est la matrice de rang r qui minimise la norme spectrale de A - B.
En ce qui concerne la preuve pour la norme de Frœbenius, on garde les mêmes notations et on remarque que
La preuve est alors similaire.
Ainsi,
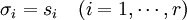
Application aux langues naturelles
Une des principales utilisation de la décomposition en valeurs singulières dans l'étude des langues naturelles est l'analyse sémantique latente (ou LSA, de l'anglais latent semantic analysis), une méthode de la sémantique vectorielle. Ce procédé a pour but l'analyse des relations entre un ensemble de documents et des termes ou expressions qu'on y trouve, en établissant des « concepts » communs à ces différents éléments.
Brevetée en 1988, on parle également d'indexation sémantique latente (LSI). Voici une description sommaire du principe de cet algorithme.
Dans un premier temps, on construit une matrice représentant les différentes occurrences des termes (d'un dictionnaire prédéterminé, ou extraits des documents), en fonction des documents. Par exemple, prenons trois œuvres littéraires :
- Document 1 : « J'adore Wikipédia »
- Document 2 : « J'adore le chocolat »
- Document 3 : « Je déteste le chocolat »
Alors la matrice M associée à ces documents sera :
-
J' Je adore déteste le Wikipédia chocolat Document 1 1 0 1 0 0 1 0 Document 2 1 0 1 0 1 0 1 Document 3 0 1 0 1 1 0 1
Éventuellement, on peut réduire certains mots à leur radical ou à un mot équivalent, ou même négliger certains termes trop courts pour avoir un sens ; la matrice contient alors Je, adorer, détester, Wikipédia, chocolat. Les coefficients (ici 1 ou 0) sont en général non pas un décompte mais une valeur proportionnelle au nombre d'occurrences du terme dans le document, on parle de pondération « tf-id » (term frequency — inverse document frequency).
Alors M sera de la forme :
On peut également travailler avec la transposée de M, que l'on note N. Alors les vecteurs lignes de N correspondent à un terme donné, et donnent accès à leur « relation » à chaque document :
Et de même, une colonne de la matrice N représente un document donné, et donne accès à sa relation à chaque terme :
On accède à la corrélation entre les termes de deux documents en effectuant leur produit scalaire. La matrice symétrique obtenue en calculant le produit S = NNT contient tous ces produits scalaires. L'élément de S d'indice (i,p) contient le produit :
-
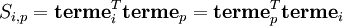
De même, la matrice symétrique Z = NTN contient les produits scalaires entre tous les documents, qui donne leur corrélation selon les termes :
-
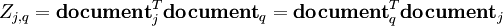
On calcule maintenant la décomposition en valeurs singulières de la matrice N, qui donne les matrices telles que :
- M = UΣVT
Alors les matrices de corrélation deviennent :
La matrice U contient les vecteurs propres de S, la matrice V contient ceux de Z. On a alors :
Les valeurs singulières,

Cinématique inverse
En robotique, le problème de la cinématique inverse, qui consiste essentiellement à savoir « comment bouger pour atteindre un point, » peut être abordé par la décomposition en valeurs singulières.
Énoncé du problème
On peut considérer — c'est un modèle très général — un robot constitué de bras articulés, indicés i, formant un angle θi entre eux, dans un plan. On note X le vecteur représentant la position du « bout » de cette chaine de bras, qui en pratique est une pince, une aiguille, un aimant… Le problème va être de déterminer le vecteur θ, contenant tous les θi, de sorte que X soit égal à une valeur donnée X0.
Résolution
On définit le jacobien de X par :
-
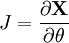
On a alors :
-
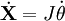
Si J est inversible (ce qui est, en pratique, toujours le cas), on peut alors accéder à la dérivée de θ :
-
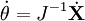
Si J n'est pas inversible, on peut de toute façon utiliser la notion de pseudo-inverse. Néanmoins, son utilisation ne garantit pas que l'algorithme converge, il faut donc que le jacobien soit nul en un nombre réduit de points. En notant (U,Σ,V) la décomposition en valeurs singulières de J, l'inverse (le pseudo-inverse si J n'est pas inversible) de J est donné par :
-
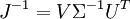
-
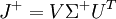
On a noté Σ+ la matrice diagonale comportant l'inverse des valeurs singulières non-nulles. Dans la suite, la notation J-1 renverra sans distinction à l'inverse ou au pseudo-inverse de J.
Le calcul des vecteurs colonne de J peut être effectué de la manière qui suit :
- On note Xi la position de l'articulation i ;
- On note ez le vecteur unitaire de même direction que l'axe de rotation de l'articulation ;
Alors
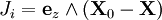
On peut alors discrétiser l'équation, en posant :
Et en ajoutant Δθ à θ à chaque itération, puis en recalculant ΔX et Δθ, on atteint peu à peu la solution désirée.
Résolution alternative
Il est également possible d'utiliser la décomposition en valeurs singulières de J autrement pour obtenir Δθ :
En multipliant successivement à gauche par J puis par sa transposée, pour enfin utiliser la décomposition en valeurs singulières de JTJ, on a :
Soit en conclusion :
-
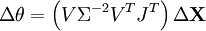
Autres exemples
Une utilisation courante de la décomposition en valeurs singulières est la séparation d'un signal sur deux sous-espaces supplémentaires, par exemple un sous-espace « signal » et un sous-espace de bruit. La décomposition en valeurs singulières est beaucoup utilisée dans l'étude de l'inversion de matrices, très pratique dans les méthodes de régularisation. On l'emploie également massivement en statistiques, en traitement du signal, en reconnaissance de formes et dans le traitement informatique des langues naturelles.
De grandes matrices sont décomposées au travers de cet algorithme en météorologie, pour l'algorithme de Lanczos par exemple.
L'étude géologique et sismique, qui a souvent à faire avec des données bruitées, fait également usage de cette décomposition - et de ses variantes multidimensionnelles - pour « nettoyer » les spectres obtenus. Étant donnés un certain nombre d'échantillons connus, certains algorithmes peuvent, au moyen d'une décomposition en valeurs singulières, opérer une déconvolution sur un jeu de données.