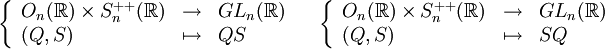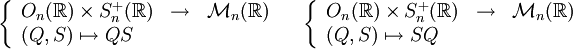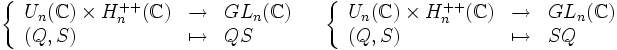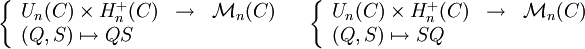Décomposition polaire - Définition

Décomposition polaire d'une matrice réelle

• Les applications suivantes sont des homéomorphismes, et même des difféomorphismes.

Autrement dit, toute matrice inversible réelle se décompose de façon unique en produit d'une matrice orthogonale et d'une matrice symétrique strictement positive.

• Les applications suivantes sont surjectives mais en général non injectives :

Exemple de décomposition polaire d'une matrice réelle

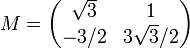
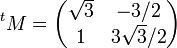
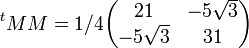
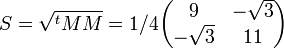
(S est bien une matrice symétrique définie positive).

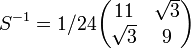
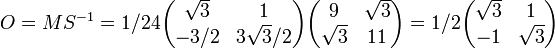
Méthode de décomposition polaire d'une matrice réelle

Soit M notre matrice à décomposer. On veut M = OS avec O matrice orthogonale et S matrice symétrique.

On calcule :

1. ^tMM = S².
2. .
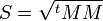
3. O = MS ^{− 1}.

Décomposition polaire d'une matrice complexe

• Les applications suivantes sont des homéomorphismes, et même des difféomorphismes.

Autrement dit, toute matrice inversible complexe se décompose de façon unique en produit d'une matrice unitaire et d'une matrice hermitienne strictement positive.

• Les applications suivantes sont surjectives mais en général non injectives :

Remarque. Pour n=1, on retrouve l'écriture z = re^iθ d'un nombre complexe non nul. C'est la raison du nom de décomposition polaire : c'est une sorte de généralisation des coordonnées polaires.