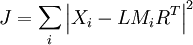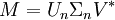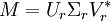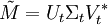Décomposition en valeurs singulières - Définition

Variantes

SVD/ICA

Il est courant d'associer les résultats de la décomposition en valeurs singulières à ceux de l'analyse en composantes indépendantes (ou ICA). Les algorithmes qui exploitent une combinaison des deux sont couramment appelés SVD/ICA. En effet, l'analyse en composantes indépendantes tient compte des termes d'ordre supérieurs ou égaux à 2 négligés par la décomposition en valeurs singulières.

Décomposition généralisée

Le procédé de décomposition en valeurs singulières généralisée, ou GSVD, étend le concept de la décomposition en valeurs singulières en utilisant des seminormes quadratiques et s'applique aux systèmes linéaires.

Une matrice A m × n et une matrice B p × n réelles ou complexes étant données, leur décomposition généralisée est :

A = UΣ₁[0,R]Q ^*

et

B = VΣ₂[0,R]Q ^*

avec U,V et Q des matrices unitaires et R une matrice triangulaire supérieure, non-singulière, carrée r × r, en notant le rang de [A ^* ,B ^* ].

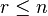
Par ailleurs, Σ₁ et Σ₂ sont des matrices m × r et p × r respectivement, nulles partout sauf sur leur diagonale principale, qui contient les réels α_i et β_i respectivement, tels que :

et .

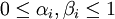
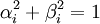
Les rapports σ_i = α_i / β_i sont analogues aux valeurs singulières. Dans le cas particulier, mais important, où B est carrée et inversible, elles sont les valeurs singulières, U U et V sont alors les vecteurs singuliers de la matrice AB ^{− 1}.

Décomposition 2D

On peut généraliser la décomposition en valeurs singulières à plusieurs dimensions, en particulier pour traiter les images. Ici, une image puis ses valeurs singulières (3DSVD). Ici encore, elles décroissent rapidement.

Il est possible d'étendre le concept de décomposition en valeurs singulières à des matrices complexes, ou, de manière équivalente à des matrices constituées de vecteurs 2D. Le calcul est proche de celui de la décomposition en valeurs singulières simple. On parle de décomposition en valeurs singulières 2D, ou 2DSVD.

De même que pour le cas simple, il existe des algorithmes spécialisés qui donnent une approximation d'un ensemble de matrices de rang faible, par exemple des images ou des cartes météorologiques.

Soit X = (x₁,...,x_n) un ensemble de réels (c'est-à-dire de vecteurs 1D). Pour la décomposition en valeurs singulières, on construit la matrice de covariance et la matrice de Gram :

F = XX^T , G = X^TX.

En calcule ensuite leurs vecteurs propres U = (u₁,...,u_n) et V = (v₁,...,v_n). Puisque VV^T = I,UU^T = I, on a :

X = UU^TXVV^T = U(U^TXV)V^T = UΣV^T.

En ne gardant que les K vecteurs propres principaux de U et V, on obtient ainsi une approximation de rang faible de la matrice X. Pour les algorithmes de 2DSVD, on travaille avec des matrices 2D, c'est-à-dire un ensemble de matrices (X₁,...,X_n) . On construit les matrices de covariance ligne-ligne et colonne-colonne  :

, .

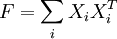
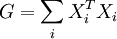
Pour ce faire, on agit de la même façon que pour la décomposition classique, et on calcule leurs vecteurs propres U et V. On approche les X_i :

X_i = UU^TX_iVV^T = U(U^TX_iV)V^T = UM_iV^T

par une méthode identique à celle de la décomposition en valeurs singulières.

On obtient ainsi une approximation de (X₁,...,X_n) par la fonction :

Les algorithmes de 2DSVD sont principalement utilisés en compression et représentation d'images. L'utilisation de la SVD pour la compression d'images a toutefois été montrée comme étant sous-optimale par rapport à une DCT, notamment à cause de l'obligation de transmettre la transformée elle-même, en plus des données image. Son rôle dans le domaine de la compression est de fait marginal.

Décomposition 3D

En considérant l'utilisation de matrices dépliées, on peut étendre la décomposition en valeurs singulières aux cas tridimensionnels, ou 3DSVD. De tels algorithmes sont utilisés en sismologie, en météorologie et en acoustique, où l'analyse de données 3D (ou 2D dépendant du temps) est souvent nécessaire.

Décompositions réduites

Dans les utilisations, il est assez rare de devoir utiliser la forme complète de la décomposition en valeurs singulières, y compris la décomposition complète du noyau sous forme unitaire. Il est en effet courant, plus rapide, et moins coûteux en termes de mémoire, d'utiliser des versions réduites de la SVD. Les décompositions suivantes sont valables pour les matrices m × n de rang r.

SVD « fine »

Seuls les n vecteurs colonnes de U correspondant aux vecteurs lignes de V* sont calculés. Les vecteurs colonnes restant de U ne sont pas calculés, ce qui économise une quantité importante de calculs si . La matrice U_n est ainsi m × n, Σ_n est diagonale n × n et V est n × n.

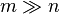
La première étape du calcul d'une SVD « fine » est la décomposition QR de M, qui peut être optimisée pour .

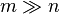
SVD « compacte »

Seuls les r vecteurs colonnes de U et les r vecteurs lignes de V* correspondants aux valeurs singulières non-nulles Σ_r sont calculés. On obtient un résultat plus rapidement qu'avec la SVD « fine » si . La matrice U_r est ainsi m × r, Σ_r est diagonale r × r et V_r* est r × n.

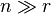
SVD « tronquée »

Seuls les t vecteurs colonnes de U et les t vecteurs lignes de V* correspondants aux t plus grandes valeurs singulières Σ_r sont calculées. C'est un calcul encore plus rapide que la SVD « fine » si . La matrice U_t est ainsi m×t, Σ_t est diagonale t × t et V_t* est t × n.

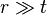
Cependant, cette décomposition « tronquée » n'est plus une décomposition exacte de la matrice d'origine M, mais la matrice obtenue, , est la meilleure approximation de M obtenue par une matrice de rang t, pour la norme d'opérateur subordonnée aux normes euclidiennes de Rⁿ et R^m.