Densité de Schnirelmann - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la densité de Schnirelmann d'une suite de nombres est une manière de mesurer de quelle façon la suite est « dense ». Elle a été nommée en l'honneur du mathématicien russe L.G. Schnirelmann, qui fut le premier à l'étudier.
Intuitivement, nous ressentons qu'il y a « plus » de nombres impairs que de carrés parfaits ; toutefois, l'ensemble des nombres impairs n'est pas « plus grand » en fait que l'ensemble des carrés parfaits : les deux ensembles sont infinis et dénombrables et peuvent par conséquent être mis en bijection. Nous avons donc besoin d'une meilleure manière pour formaliser notre notion intuitive. C'est ce qu'effectue la densité de Schnirelmann.
Définition
Soit
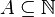
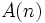
![A \cap [1, n]](https://static.techno-science.net/illustration/Definitions/autres/b/be15c18a6e37263e659ce5732fa8b901_cb42a86c96b1f3ba10fc703d7ee44cc0.png)
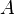
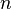
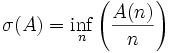
c’est-à-dire la borne inférieure de l'ensemble
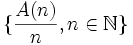
Cette définition permet de dire que cette densité existe à chaque fois et qu'elle est unique, puisque tout sous-ensemble minoré de

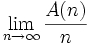
Par exemple, l'ensemble des nombres impairs possède une densité de Schnirelmann de

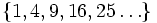
Théorèmes de Schnirelmann
Si nous posons
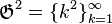
-
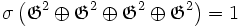
où
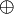
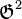
Il est clair que
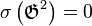
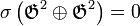
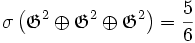
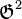
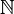
Schnirelmann réussit à développer cette idée dans les théorèmes suivants, en se dirigeant vers une théorie additive des nombres, et démontra qu'ils étaient une nouvelle ressource (potentiellement puissante) pour attaquer d'importants problèmes, tels que le problème de Waring et la conjecture de Goldbach.
Le premier théorème est une formulation plus faible du théorème de Mann :
- Soient
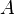
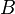
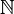
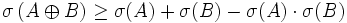
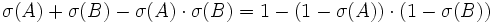
- Soit
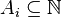
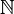
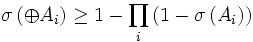
Ce théorème fournit le premier aperçu du comportement d'accumulation des sommes d'ensembles. Il semble malheureux que sa conclusion arrive avant de montrer que
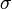
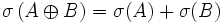
- Soient
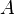
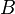
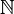
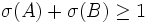
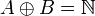
- Soit
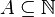
 , alors il existe un entier
, alors il existe un entier
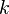
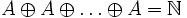
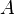
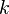
Ce dernier théorème est explicitement connu comme « Théorème de Schnirelmann ».
Une application de ce théorème permet d'exprimer tout nombre entier comme somme de nombres premiers : soit
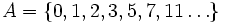
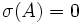
 . Par application du théorème de Schnirelmann, il existe un nombre entier
. Par application du théorème de Schnirelmann, il existe un nombre entier
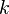
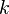
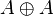
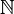


Ce nombre