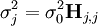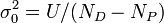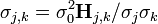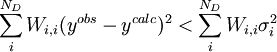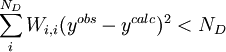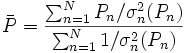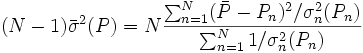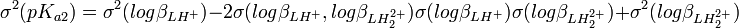Détermination des constantes d'équilibre - Définition
La liste des auteurs de cet article est disponible ici.
Analyse des résultats
Fiabilité de la détermination et affinement du modèle
Une détermination numérique constitue un test d'un modèle, et non pas une preuve de sa pertinence. On peut examiner la fiabilité du modèle à l'aide de l'accord-type, des incertitudes et des corrélations et songer à modifier le modèle pour une détermination plus fiable. Cependant, la détermination cesse alors d'être une mesure de constantes d'équilibres connus et risque de devenir une découverte d'équilibres. Cela doit se faire sagement, en se guidant avec des comparaisons impartiales entre modèles.
L'incertitude dans la valeur du j ième paramètre P est fournie par le j, j ième élément (le j ième sur la diagonale) de la matrice
où σ0 est l'incertitude d'une observation à pondération 1, l'accord-type, qui peut être estimé (selon Alcock et al., 1978) avec
pour NP paramètres déterminés à partir de ND données expérimentales.
D'un point de vue statistique, l'incertitude dans la valeur d'un paramètre dénote une plage de valeurs, la taille de laquelle dépendra du niveau de confiance que l'on désire, qui générera des modèles indiscernables. Ainsi, les incertitudes reflètent l'incapacité des valeurs des paramètres de reproduire les données. Inversement, les incertitudes reflètent l'incapacité des données expérimentales de préciser les valeurs des paramètres. Certaines modifications à la conception ou à la conduite de l'expérience pourraient plus précisément établir les valeurs des paramètres incertains. Autrement, il se peut qu'un paramètre hautement incertain puisse être laissé tomber du modèle chimique sans dégradation 'importante' de l'accord du modèle avec les données.
Les coefficients de corrélation entre les valeurs des paramètres sont rapportés par les éléments hors-diagonale de la matrice
Ceux-ci reflètent l'interdépendance des paramètres en modélisant les données, i.e. l'importance d'inclure chaque paramètre dans le modèle chimique. Inversement, les coefficients de corrélation reflètent l'incapacité des données à différencier entre les paramètres. Ici encore, certaines modifications expérimentales pourraient y remédier, mais il se peut qu'une paire de paramètres dont les valeurs sont hautement co-reliées puisse être remplacée dans le modèle chimique par un seul paramètre, sans dégradation 'importante' de l'accord du modèle avec les données.
Par ailleurs, il se peut que le modèle chimique donne un accord 'insatisfaisant' avec les données, selon la taille du σ0 et celle des résidus, mais il serait utile de savoir ce qui constitue un accord 'satisfaisant'. Selon Hamilton (1964), si la condition pour ND données
est remplie, l'accord est satisfaisant. La quantité σi représente l'incertitude anticipée sur la i ième mesure. Si l'on suit la pratique prescrite ci-haut, on anticipera les valeurs de ces σi en prédisant à quel degré les erreurs expérimentales (estimées et anticipées) dans les paramètres fixes Q affecteront les mesures prédites (ycalc). Si, aussi, on utilise ces σi dans les pondérations, avec
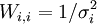
ou, écrit plus simplement, U < ND pour ND données. C'est-à-dire qu'un accord satisfaisant donne des écarts entre mesures (
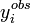
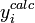
Dans le cas d'un accord insatisfaisant, l'inclusion d'autres espèces (et d'autres paramètres β) pourrait l'améliorer. Étant donné que l'ajout d'un paramètre d'habitude améliorera l'accord, alors que l'élimination d'un paramètre d'habitude l'empirera, il devient important de comprendre ce qui constitue une dégradation ou amélioration 'importante'. Une altération d'un modèle chimique, surtout l'inclusion d'une espèce inattendue ou la mise de côté d'une espèce attendue, doit être guidée par le bon sens chimique et être impartial. Pour aider une décision impartiale si l'on expérimente avec divers modèles chimiques, le test de Hamilton (Hamilton, 1964) utilisé couramment en cristallographie, permet aux données de décider si un modèle alternatif devrait être rejeté ou accepté.
Finalement, les mesures elles-mêmes ainsi que les paramètres Q influenceront la qualité de l'accord. Par exemple, certaines données extrêmes ou aberrantes peuvent être 'problématiques' en ce que leur mise à l'écart améliore de façon 'importante' la qualité de l'accord, et ainsi réduit les incertitudes dans les P, contrairement à la règle générale que l'accord et les incertitudes seront améliorés par un plus grand nombre de données. Par ailleurs, les résidus yobs − ycalc peuvent être co-reliés, c'est-à-dire que les yobs ne sont pas distribués de façon aléatoire de part et d'autre des ycalc, ce que la méthode des moindres carrés supposera. Pour remédier à de tels problèmes, on peut omettre certaines données, ou déplacer la pondération en changeant les σ(Q), ou changer les Q eux-mêmes, ou même les affiner aux côtés des paramètres P comme s'ils devaient être déterminés (ce que certains logiciels permettent). Ce genre de bricolage pour la simple amélioration de l'accord biaise le modèle au risque d'une perte de sens. Le bon sens chimique, plutôt qu'un penchant pour un résultat, devrait guider tout changement au modèle, aux paramètres fixes, aux données ou à leur pondération, et le mal que l'on se donnerait pour améliorer un accord ou un modèle pourraient être orientés à améliorer la qualité des données (i.e. la confiance en elles).
Toutefois, il peut être utile parfois de rigoureusement comparer les résultats découlant d'altérations judicieuses au modèle. L'omission ou la désaccentuation de données et l'altération de paramètres fixes donnent lieu à des modèles compétiteurs où les matrices
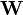
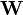
Erreurs expérimentales
Comme indiqué plus tôt, les incertitudes calculées avec la matrice
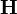
L'estimation de 'l'erreur expérimentale' dans une constante d'équilibre peut donc se faire à l'aide d'une seule valeur de σ provenant d'une seule détermination, ou de plusieurs déterminations répétées pour amoindrir les effets d'erreurs aléatoires dans certaines sources d'erreurs systématiques Q, jusqu'à la combinaison d'expériences complètement indépendantes où les effets de toutes les sources d'erreurs systématiques seront amoindris. Donc, toute estimation 'd'erreur expérimentale' devrait aussi communiquer la diversité des données utilisées pour l'estimation. Toutefois, la simple prise d'une moyenne des valeurs séparément déterminées ne tiendra pas compte de la fiabilité inégale des déterminations, telle que rapportée par les incertitudes calculées dans chaque détermination. Plutôt, la moyenne
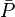
où σn(Pn) rapporte l'incertitude de la n ième de N déterminations d'un même paramètre P. Pourvu que les tailles relatives des pondérations soient justes, cette moyenne sera insensible aux valeurs absolues de ces pondérations. De même, on peut quantifier 'l'erreur expérimentale' du
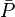
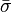
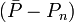
Constantes dérivées et modèles équivalents
Si l'on calcule une constante d'équilibre qui est fonction de constantes de formation que l'on a déterminées, telle qu'un Ka, l'incertitude d'une telle constante dérivée n'est pas une simple fonction des incertitudes dans les constantes déterminées, comme le voudraient les règles normales de la propagation d'erreurs, puisque cela requiert que les sources d'erreur soient indépendantes alors que les constantes déterminées par les mêmes données sont co-reliées. En guise d'exemple, pour la protonation d'une substance dibasique L,
-
![K_{a1} = \frac {[LH^+]}{[H^+][L]} = \beta_{LH^{+}}](https://static.techno-science.net/illustration/Definitions/autres/d/d31bd239ad5acc2fd53f1b6ff75f8e15_6ca714e4e543412253082c796d7649f3.png)
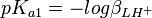
-
![K_{a2} = \frac {[H^+][LH^+]}{[LH_2^{2+}]} = \frac {[H^+]^2[L]}{[LH_2^{2+}]} \frac {[LH^+]}{[H^+][L]} = \frac {\beta_{LH^{+}}}{\beta_{LH_2^{2+}}}](https://static.techno-science.net/illustration/Definitions/autres/8/8d2c95fafd00f55a91a3f4daecee42ce_1b0c5a354c5bc128c43538e5a9a9cada.png)
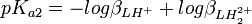
L'incertitude et la variance sur la valeur de pKa1 sont les mêmes que sur
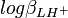
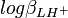
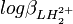
où
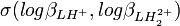
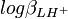
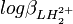
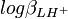
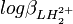
Les constantes dérivées constituent une représentation équivalente d'un modèle chimique. Dans cet exemple, pKa1 et pKa2 peuvent entièrement et de façon entièrement équivalente remplacer
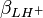
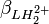
Parfois même, un modèle construit d'équilibres de formation (avec constantes β) n'est pas le mieux adapté au système expérimental. Tout équilibre de formation présume que les concentrations des réactifs libres ne seront pas négligeables alors que, dans bien des cas, les constantes de formation sont tellement grandes qu'il ne reste presque plus de l'un ou d'un autre réactif en forme libre. Cela peut donner des difficultés pendant les calculs des concentrations, des valeurs de β très incertaines et un calcul de constantes dérivées qui met en œuvre des constantes β très incertaines.
Potvin (1990b) a présenté une manière de construire des modèles équivalents, d'en déduire les rapports d'erreur et d'éviter de devoir composer avec des concentrations négligeables en réactifs libres.