Division harmonique - Définition

Conjugué harmonique

Définition

Soient trois points A, B et I distincts alignés. Un simple calcul vectoriel ou barycentrique montre que, si I n'est pas le milieu de [AB], il existe un unique point J tel que I et J divisent harmoniquement [AB]. Le point J est appelé conjugué harmonique de I par rapport à A et B. D'après ce qui précède, si J est le conjugué harmonique de I par rapport à deux points donnés, I est le conjugué harmonique de J par rapport à ces mêmes points.

Il est naturel d'étendre la relation de conjugaison aux points A et B en prenant chacun d'entre eux égal à son conjugué (écrire la condition de division harmonique comme une égalité de produits).

Dans le cadre du plan projectif, vu comme complété du plan affine, on ajoute un point à l'infini pour la direction de la droite passant par A et B. Ce point est naturellement le conjugué harmonique du milieu de A et B par rapport à A et B. Ceci apparait dans la construction qui suit.

Construction géométrique

On peut construire le conjugué harmonique en exploitant une propriété des faisceaux harmoniques, qui seront étudiés à la section suivante. Appelons pour le moment faisceau harmonique quatre droites sécantes en un même point, et telles qu'il existe une sécante à ces quatre droites qui coupent celles-ci en quatre points en division harmonique (l'ordre des droites n'est pas indifférent, voir section suivante). On montre alors (voir figure jointe) que :

Proposition. — Un faisceau de quatre droites est harmonique si et seulement si une parallèle à l'un de ses rayons est divisée par les trois autres en deux segments égaux.

Étant donné trois points distincts A, B et I sur une droite, tels que I ne soit pas le milieu de A et B, on peut trouver le point J conjugué harmonique de I par rapport à A et B en construisant un faisceau harmonique [MA, MB, MI, MJ’] comme suit :

• soit M un point non aligné avec les précédents ; la parallèle à (MA) passant par B coupe donc (MI) en un point que l'on appelle I’ ;

• soit J’ le symétrique de I’ par rapport à B, alors (MJ’) coupe (AB) en J qui est le point cherché. En effet si (MJ’) et (AB) étaient parallèles, AMBJ’ serait un parallélogramme, et donc AMBI’ également, et le point I, intersection des diagonales de ce dernier, serait milieu de A et B.

Cette construction fournit une démonstration géométrique de l'existence du conjugué harmonique, mais aussi de son unicité (la propriété utilisée est une condition nécessaire est suffisante). Quand I est le milieu de A et B, la droite (MJ’) est parallèle à la droite (AB), ce qui est cohérent avec le choix du point à l'infini comme conjugué en géométrie projective.

On peut également construire le conjugué harmonique par la polaire, en n'utilisant que la règle (voir ci-dessous).

Cercles orthogonaux, points conjugués

Soit (C) un cercle et M et M’ deux points tels que la droite (MM’) coupe le cercle (C) en deux points A et B distincts. Alors le cercle (C’) de diamètre [MM’] est orthogonal à (C) si et seulement si [MM’] divise harmoniquement [AB].

On dit alors que M et M’ sont conjugués par rapport au cercle (C).

Démonstration : Soit O et O’, les centres de (C) et (C’), O’ est donc le milieu de [MM’]. Soient R et R’ leurs rayons ; on a (cf. puissance d'un point par rapport à un cercle :

.

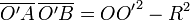
Les deux cercles sont orthogonaux si et seulement si O’O²=R²+R’² (angle droit au point de contact), et donc si et seulement si :

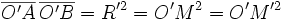
On en déduit que les deux cercles sont orthogonaux si et seulement si la division est harmonique d'après la relation de Newton (voir plus haut).

La définition peut s'étendre aux cas où la droite (MM’) ne coupe pas le cercle (C) : deux points M et M’ seront dit conjugués par rapport à un cercle (C) si le cercle de diamètre [MM’] est orthogonal à (C).

Propriété. — Deux points sont conjugués par rapport à un cercle de centre O si et seulement si :

.

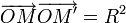
Soit O' le milieu de [MM’], et donc le centre du nouveau cercle, et T un point d'intersection entre les deux cercles, en particulier OT²=R². En utilisant ceci on obtient :

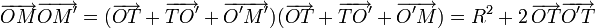
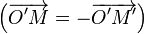
d'où le résultat.

L'ensemble des conjugués d'un point par rapport à un cercle est la polaire de ce point par rapport au dit cercle.