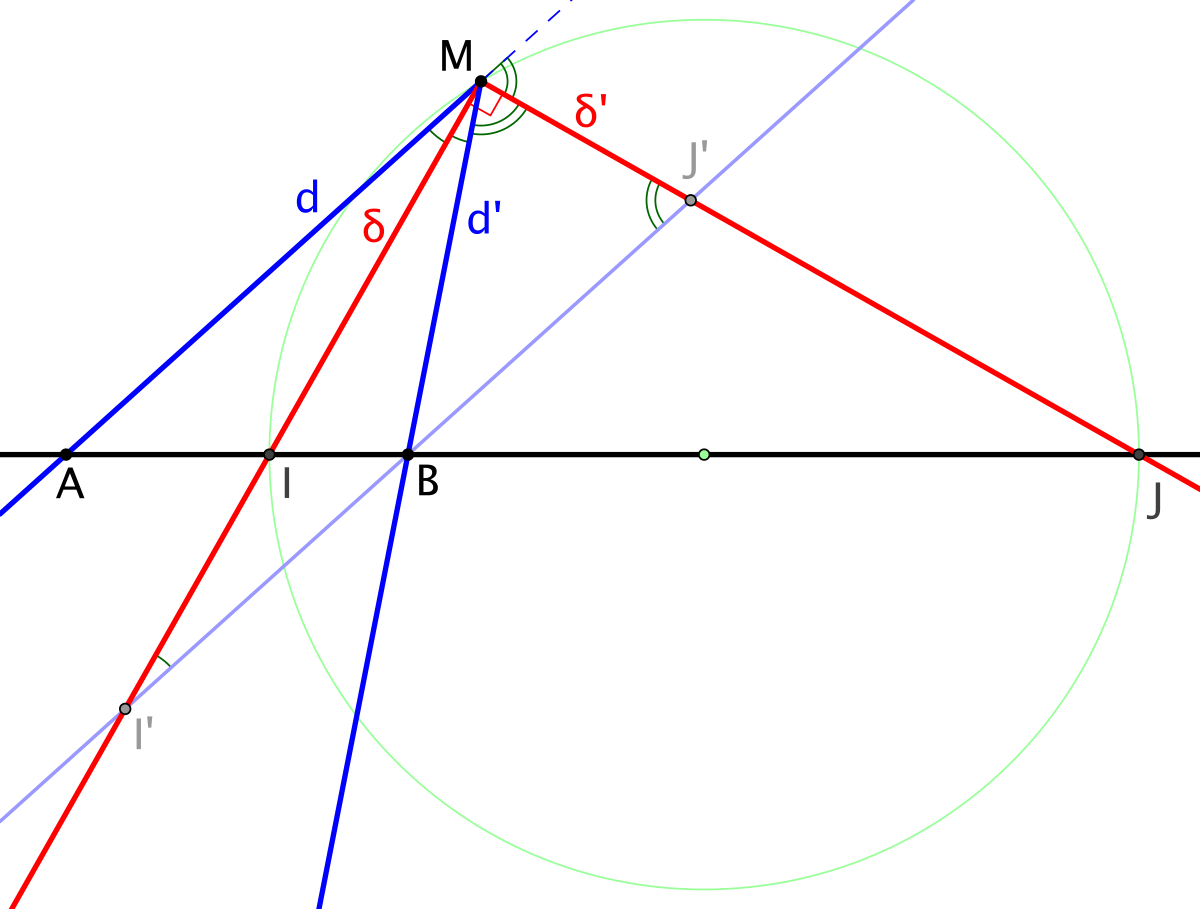
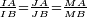Division harmonique - Définition
La liste des auteurs de cet article est disponible ici.
Quelques exemples en géométrie euclidienne
Les bissectrices
On déduit immédiatement de la première proposition énoncée sur les faisceaux harmoniques (section « construction géométrique »), que si quatre droites concourantes d, d’, δ et δ' sont telles que δ' est la symétrique de δ par rapport à d’ et parallèlement à d , alors (d, d’, δ, δ') est un faisceau harmonique et réciproquement (c'est en fait juste une autre façon d'énoncer cette proposition).
En géométrie euclidienne, en prenant une symétrie orthogonale, on obtient le cas particulier suivant :
- deux droites d et d’ et leurs deux bissectrices δ et δ' forment un faisceau harmonique (d, d’, δ, δ').
Supposons maintenant que d et d’ sont les deux côtés issus de M d'un triangle ABM. Les bissectrices intérieure δ et extérieure δ' coupent le côté (AB) en I et J. On a donc que I et J divisent harmoniquement le segment [AB].
Adaptée à ce cas particulier, la démonstration de la propriété se ferait en construisant une parallèle à la bissectrice extérieure passant par B (ou par A). Reprenons la même démonstration, mais en construisant une parallèle au côté (MA) passant par B, qui coupe donc les deux bissectrices δ, δ' en deux points I’ et J’ de façon que B soit le milieu de I’ et J’, puisque (d, d’, δ, δ') est un faisceau harmonique. Du fait que les deux bissectrices sont orthogonales on a de plus que, le triangle I’MJ’ étant rectangle en M, MB = BI’=I’B. Si l'on veut repartir de zéro, on peut aussi déduire ceci du fait que, δ et δ' étant les bissectrices de d et d’, par des considérations sur les angles, les deux triangles I’BM et J’BM sont isocèles en B.
En appliquant deux fois le théorème de Thalès tout comme dans la preuve initiale, on obtient alors une égalité supplémentaire :
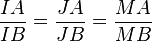
On en déduit que, deux points A et B étant donnés, l'ensemble des points M tels que le rapport de longueurs MA/MB est constant différent de 1 est un cercle de diamètre [IJ], où J et I divisent harmoniquement [AB]. Si la constante est k > 0, k ≠ 1, les points I et J sont les deux seuls points de la droite (AB) tels que
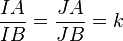
En effet, si MA/MB=k, d'après l'égalité précédente, les bissectrices de l'angle en M coupent bien la droite (AB) en I et J qui divisent harmoniquement [AB], et comme les deux bissectrices sont orthogonales, le point M est sur le cercle de diamètre [IJ] (voir cercle circonscrit).
Réciproquement, si M est sur le cercle de diamètre [IJ], et différent de I et J, la parallèle à (MA) passant par B coupe les droites (MI) et (MJ) en deux points que nous nommons I’ et J’, et B est le milieu de I’ et J’, puisque (A, B, I, J) est une division harmonique. Le triangle MI’J’ étant rectangle en M, car M est sur le cercle de diamètre [IJ] (voir cercle circonscrit), BM = BI’ = BJ’ ; les triangles MBI’ et MBJ’ sont alors isocèles en B, et par parallélisme (MI) et (MJ) sont les bissectrices en M du triangle AMB. On en a déduit alors que MA/MB=IA/IB = JA/JB = k.
Le point M étant fixé, ce cercle est le cercle d'Apollonius du triangle ABM passant par M.
La droite d'Euler
Toujours en Géométrie euclidienne, on montre que dans un triangle, le centre de gravité G, l'orthocentre H, le centre du cercle circonscrit Ω, et le centre du cercle d'Euler E sont tous les quatre alignés sur une droite dite droite d'Euler du triangle, de plus ils sont en division harmonique (dans cet ordre). Ceci résulte de ce que H a pour image Ω et Ω pour image E par une même homothétie de centre G et de rapport -1/2.