Parallélogramme - Définition

Un parallélogramme, en géométrie, est un quadrilatère (convexe) dont les côtés sont parallèles deux à deux ; c'est un trapèze particulier.

Propriétés

• Les diagonales d'un parallélogramme se coupent en leur milieu.
• Le point d'intersection de ses diagonales est son centre de symétrie et de gravité.
• Ses côtés opposés ont la même longueur.
• Ses angles opposés ont la même mesure.
• Ses angles consécutifs sont complémentaires (additionnés, ils font 180°).
• Les aires des triangles qui le compose sont egales
• Ses côtés opposés sont paralleles.

Reconnaître un parallélogramme

Les propriétés précédentes peuvent aussi servir à reconnaître un parallélogramme dans un quadrilatère donné, en voici une autre :

• Il est non croisé et deux côtés opposés sont parallèles et de même longueur (on reconnaît ici la définition vectorielle).

• Les losanges, les rectangles et les carrés sont des parallélogrammes particuliers.

Aire d'un parallélogramme

Soient la longueur d'un côté du parallélogramme et la longueur de la hauteur associée.L'aire du parallélogramme vaut :

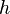
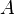
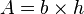
Aspect abstrait

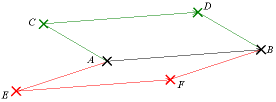
La notion de parallélogramme permet de définir la relation d'équipollence de deux bipoints, ce qui amène à la notion de vecteur en géométrie euclidienne :

• on appelle bipoint tout couple de points (l'ordre des points a une importance) ;
• deux bipoints (A,B) et (C,D) sont dits équipollents si ABDC est un parallélogramme, éventuellement aplati ;

on peut dire de manière équivalente que (A,B) et (C,D) sont équipollents si [AD] et [BC] ont le même milieu (ce qui règle le problème des parallélogrammes aplatis) ;

dans ce cas, les segments [AB] et [CD] sont parallèles et de même longueur, mais pas seulement : ils ont aussi " le même sens ".

La relation d'équipollence est une relation d'équivalence.

• on appelle vecteur la classe d'équivalence des bipoints équipollents à (A,B) ;

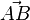
le vecteur est l'ensemble des bipoints satisfaisant la relation d'équipollence avec (A,B).

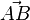
Une variante amusante

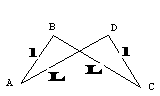
L'antiparallélogramme est un quadrilatère croisé qui possède 2 petits côtés et 2 grands côtés dans lequel les 2 grands côtés sont croisés. Il possède une propriété intéressante.