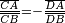Division harmonique - Définition

Introduction

(A, B, C, D) est une division harmonique :

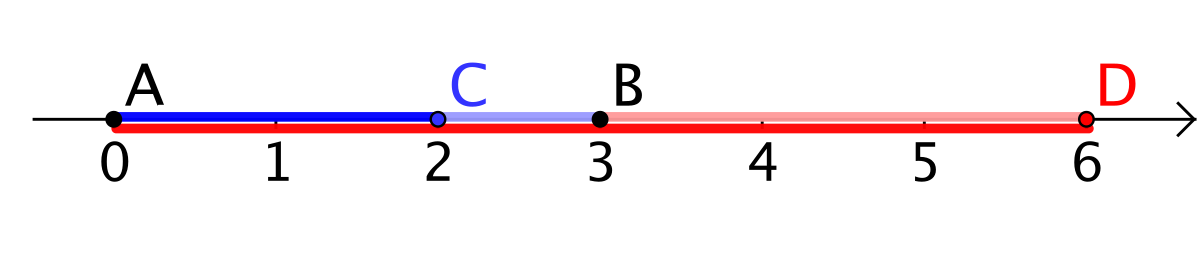
En géométrie affine quatre points alignés sont en division harmonique quand ils vérifient l'égalité des rapports de mesure algébrique indiquée ci-contre. Elle apparait naturellement dans plusieurs figure géométriques, par exemple le quadrilatère complet. C'est plus fondamentalement une notion de géométrie projective, puisqu'il s'agit d'exprimer qu'un birapport vaut -1.

Elle permet de définir la conjugaison harmonique, que l'on retrouve dans la conjugaison par rapport à deux droites, par rapport à un cercle, et plus généralement par rapport à une conique, c'est-à-dire (en projectif) à l'orthogonalité par rapport à la forme quadratique qui la définit.

Points en division harmonique

On dit que le réel b est moyenne harmonique de c et d si .

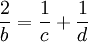
Quatre points A,B,C,D (dans cet ordre) d'une droite sont dit en division harmonique si est moyenne harmonique de et ; soit

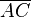
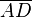
relation de Descartes : .

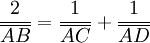
On peut encore écrire cette relation sous la forme c'est-à-dire que l'on préfère mettre sous la forme .

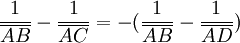
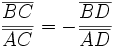
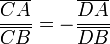
La quantité qui dans le cas présent prend la valeur -1 se nomme le birapport ou rapport anharmonique des quatre points et c'est un invariant intéressant en géométrie projective.

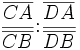
On dit également que C et D divisent harmoniquement le segment [AB] ; du fait du signe du birapport, l'un de ces deux points est à l'intérieur du segment [CD] et l'autre à l'extérieur, de plus les rapports de longueur CA/CB et DA/DB sont égaux.

La relation a plusieurs symétries : si A et B divisent harmoniquement [CD], alors d'une part B et A également, d'autre part C et D divisent harmoniquement [AB]. La division harmonique ne dépend donc que des deux paires de points, {A,B} et {C,D}, l'ordre entre les deux paires et à l'intérieur de celles-ci étant indifférent, ce qui fait 8 permutations (identité comprise) sur les 24 possibles. On montre que les 16 autres permutations ne conservent pas la division harmonique : l'ordre entre les quatre points n'est pas indifférent.

On prouve facilement qu'une suite de quatre points alignés (A,B,C,D) est en division harmonique si et seulement si l'une des relations suivantes est vérifiée :

relation de Newton : où I est le milieu de [AB] ;

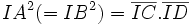
relation de Mac-Laurin : où J est le milieu de [CD].

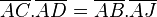
Faisceau harmonique de droites

Définition et propriété caractéristique

La définition de faisceau harmonique dans le plan affine est un peu plus générale que celle donnée au paragraphe précédent : il s'agit de quatre droites dans un ordre donné, sécantes en un même point ou toutes parallèles (c'est-à-dire sécantes en un même point à l'infini dans le plan projectif vu comme complété du plan affine), et telles qu'il existe une sécante à ces quatre droites qui intersecte celles-ci en une division harmonique, les 4 points étant bien sûr pris dans le même ordre que les droites auxquelles ils appartiennent.

Quand les quatre droites sont parallèles, toute sécante est alors découpée par celles-ci en une division harmonique, d'après le théorème de Thalès qui donne la conservation des rapports de mesure algébrique en jeu.

Quand les droites sont issues d'un même point, les rapports ne sont plus conservés, mais les birapports si.

Proposition. — Considérons un faisceau de quatre droites D₁, D₂, D₃, D₄ issues d'un point O. On suppose qu'une droite D les coupe en des points M₁, M₂, M₃, M₄ formant une division harmonique, alors il en sera de même pour toute droite D’, qu'elle soit sécante aux quatre droites ou parallèle à l'une d'entre elles (avec l'interprétation donnée plus haut).

Cette propriété ne dépend donc que de la position relative des droites du faisceau, et justifie qu'il soit alors qualifié d'harmonique. La propriété reste vraie (c'est ainsi qu'on l'a démontrée) pour une sécante parallèle à l'une des droites du faisceau, en étendant aux milieux et point à l'infini la notion de division harmonique.

On la démontre à partir de la propriété énoncée à la section précédente : il suffit de l'appliquer deux fois, pour chacune des deux sécantes, relativement à deux parallèles au même rayon. On conclut alors par Thalès.

Il s'agit cependant d'un cas particulier de conservation des birapports, que l'on peut démontrer de façon analogue, voir Faisceau harmonique.

On peut voir aussi cette propriété comme une conservation de la division harmonique par projection conique, ce qui justifie qu'il s'agit bien d'une notion de géométrie projective.

Autres propriétés

On peut montrer que, dans le plan projectif, la notion de faisceau harmonique est la notion duale de celle de division harmonique. Même si on reste en géométrie affine, on retrouve des propriétés analogues, à commencer par celles de symétries (directement, par la définition). On montre également que :

Étant données 3 droites distinctes concourantes a, b et c, il existe une unique droite d telle que (a, b, c, d) sont en division harmonique. La droite d est la conjuguée harmonique de c par rapport à a et b.

En effet, soit O le point de concours des trois droites a, b et c. La droite d doit passer par 0. Soit e une sécante aux trois droites a, b et c en trois point A B et C. Si B est le milieu de A et C, d est nécessairement la parallèle à e passant par 0 et cette droite convient, d'après la propriété caractéristique ci-dessus. Si B n'est pas le milieu de A et C, soit D le conjugué harmonique de C par rapport à A et B, la droite d est alors nécessairement la droite (OD) et celle-ci convient par la propriété caractéristique.

Polaire d'un point par rapport à deux droites

Cette dernière propriété va être utile pour définir la polaire d'un point par rapport à deux droites. Mais étendons d'abord la définition de conjugué harmonique.

Définition. — Étant donné deux droites distinctes d et d' et deux points M et M’ distincts non situés sur ces droites, la droite (MM’) rencontre respectivement d et d' en P et P’ distincts. On dit que M et M’ sont conjugués harmoniques par rapport à d et d' si [M, M’, P, P’] forme une division harmonique (M et M’ sont conjugués harmoniques par rapport à P et P’).

Proposition. — Étant donné deux droites d et d' distinctes et concourantes en un point I du plan affine et un point M non situé sur ces droites, l'ensemble des conjugués harmoniques du point M par rapport à d et d' est une droite passant par I.

En effet tout point sur la conjuguée harmonique de la droite (IM) par rapport à d et d’ convient, de par la propriété caractéristique des faisceaux harmoniques. Réciproquement, si M’ est conjugué harmonique de M par rapport à d et d’, (d, d’, (IM), (IM’)) est un faisceau harmonique.

Construction de la polaire du point M par rapport aux deux droites d (portant P et Q) et d’ (portant P’ et Q’). La polaire est la droite (IJ).

Définition. — On appelle cette droite la polaire du point M par rapport aux droites d et d’.

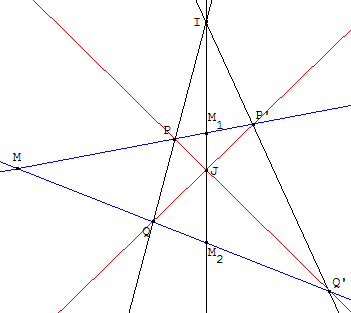
Construction de la polaire. — Étant donné deux droites d et d’ distinctes, concourantes en un point I, et un point M non situé sur ces droites, placer deux points P et Q, distincts de I, sur d et tracer les deux droites (MP) et (MQ). Les points P et Q sont supposés choisis de telle façon que ni (MP), ni (MQ) ne soient parallèles à d’. Ces droites coupent d' respectivement en P’ et Q’. Les droites Δ = (PQ’) et Δ' = (P’Q) se coupent en J. La droite (IJ) est la polaire de M par rapport à d et d’.

En effet si M₁ est le conjugué de M par rapport à P et P’ et M₂ le conjugué de M par rapport à Q et Q’, la polaire de M par rapport à d et d’ est la droite (M₁M₂) ; les points I, M₁ et M₂ sont donc alignés.
De même la polaire de M par rapport à Δ et Δ' est la droite (M₁M₂) ; les points J, M₁ et M₂ sont donc également alignés et la polaire de M par rapport à d et d’ est bien la droite (IJ).

On a obtenu une figure à 4 côtés, les droites d, d’, Δ et Δ' que l'on appelle quadrilatère complet, dont les sommets sont les 6 points d'intersection des 4 côtés, I, P, P’, J, Q et Q’, et les 3 diagonales (PP’), (QQ’) et (IJ). On a en fait démontré au passage une propriété célèbre des quadrilatères complets, à savoir que deux diagonales, par exemple (PP’) et (IJ) découpent la troisième, dans ce cas (QQ’), en deux points M et M₂, de façon que (Q, Q’, M, M₂) soit une division harmonique.

Quadrilatère complet

La propriété des quadrilatères complets vue ci-dessus peut s'énoncer ainsi.

Chacune des trois diagonales d'un quadrilatère complet est divisée harmoniquement par les deux autres.

La démonstration faite au paragraphe ci-dessus se transpose telle quelle. On aurait pu tout aussi bien démontrer la propriété pour les quadrilatères complets et l'utiliser pour la construction de la polaire.