Topologie faible - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la topologie faible d'un espace vectoriel topologique E est une topologie définie sur E au moyen de son dual topologique E' . On définit également sur E' une topologie dite faible-* au moyen de E.
Topologie affaiblie d'un espace normé
Définition
Soient E un espace vectoriel normé (réel ou complexe), ou plus généralement un espace vectoriel topologique, et E' son dual topologique, c’est-à-dire l'ensemble des formes linéaires continues sur E. Supposons que le dual E' de E sépare les points de E (i.e
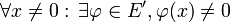
En particulier, une suite
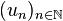
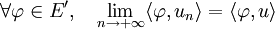
Par opposition, la topologie originelle de E s'appelle topologie forte.
Exemple
Soit E l'espace des suites réelles x = (xn) de limite nulle, muni de la norme
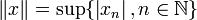

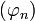
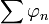
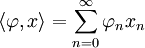
.
Pour n entier, soit en l'élément de E consistant en une suite de réels tous nuls sauf le n-ème terme qui vaut 1. Alors
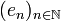
Propriétés élémentaires
- La convergence forte dans E implique la convergence faible. Par exemple, si E est normé :
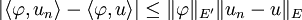
- Le dual de E pour la topologie faible est le même que le dual de E pour la topologie forte.
- La norme de la limite faible d'une suite (un)n dans E est inférieure à la limite inférieure des normes de un. Ce résultat utilise le théorème de Hahn-Banach.
- Le théorème de Hahn-Banach est également utilisé pour montrer que les sous-espaces vectoriels fermés de E sont les mêmes pour les deux topologies. Il en est de même plus généralement des parties fermées convexes.
- La topologie faible est uniformisable.
Continuité des opérateurs et topologie faible
Théorème — Soit E et F des espaces de Banach et T un opérateur linéaire fortement continu de E dans F. Alors T reste continu lorsque l'on munit E et F de leur topologie faible.
La réciproque est fausse. Un opérateur peut être continu pour les topologies faibles de E et F sans être continu pour les topologies fortes.
Topologie faible-* du dual
Définition
Il existe sur le dual E' au moins trois topologies.
- La topologie forte, définie par la famille de semi-norme
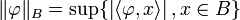
- La topologie faible de E' définie par les éléments de E'' (au même titre que la topologie faible de E est définie à partir des éléments de E').
- Comme E s'identifie à un sous-espace vectoriel de son bidual E'', on définit une topologie sur E', a priori encore plus faible que la topologie faible et appelée topologie faible-*, par la donnée des semi-normes
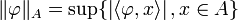

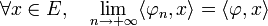
Les trois topologies, forte, faible et faible-* sont en général distinctes. Dans le cas d'un espace de Banach réflexif (identifiable à son bidual), les topologies faible et faible-* sont égales.
Exemple
Soit E l'espace
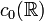
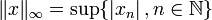
Son dual E' est l'espace
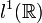
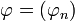
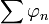
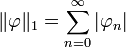
Le bidual E'' est l'espace
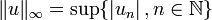
On a
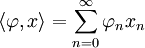
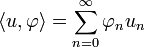
Considérons dans E' l'élément en dont les n-premiers termes valent

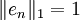
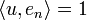
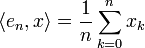
Propriétés
- Le dual topologique de E' muni de la topologie faible-* n'est autre que E lui-même.
- Soient E et F deux espaces munis de leur topologie faible, et soient F' et E' munis de leur topologie faible-*. Alors la transposée établit une bijection entre l'espace vectoriel des applications faiblement continues de E dans F, et l'espace vectoriel des applications faiblement-* continues de F' dans E'.
Théorème de Banach-Alaoglu-Bourbaki
Le théorème suivant, qui permet parfois de pallier l'absence de compacité pour la topologie forte dans les espaces de Banach de dimension infinie est la principale justification de la définition de la topologie faible-* :
Théorème — Soit E un espace normé. Alors la boule unité fermée de E' est compacte pour la topologie faible-*.
En particulier, si E est séparable, alors la boule unité du dual est séquentiellement compacte pour la topologie faible-*. En d'autres termes, toute suite (un)n bornée de E' admet une sous-suite convergente pour la topologie faible-*.
Ce théorème permet d'en déduire une caractérisation des espaces normés réflexifs (égaux à leur biduaux). Un tel espace est nécessairement un espace de Banach.
Théorème — Soit E un espace normé. Alors E est réflexif si et seulement si sa boule unité fermée est compacte pour la topologie faible.
À extraction près, une suite bornée d'un espace de Banach reflexif converge toujours faiblement (mais pas forcément fortement). Il existe de nombreuses méthodes récentes, développées notamment pour leurs applications dans le cadre de la théorie des équations aux dérivées partielles pour étudier le défaut de compacité d'une telle suite, en particulier dans les espaces de Hilbert (principe de concentration compacité de Pierre-Louis Lions, de mesure de défaut micro-locale de Patrick Gérard et Luc Tartar).
Convergence faible et espaces de Hilbert
Par le théorème de représentation de Riesz la définition de la convergence faible d'une suite (un)n sur un espace de Hilbert H s'écrit:
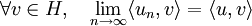
Ici
L'espace H est réflexif donc d'après le théorème de Banach-Alaoglu, un borné pour la topologie forte qui est fermé pour la topologie faible est compacte pour la topologie faible. Ainsi, dans un espace de Hilbert toute suite bornée admet une sous-suite faiblement convergente.
Mentionnons cette caractérisation élémentaire mais intéressante de la convergence forte dans un espace de Hilbert.
Proposition — Soit (un)n une suite d'éléments de H convergeant faiblement vers un élément u de H. Alors cette convergence est forte si et seulement si :
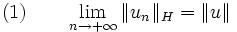
La condition (1) est évidemment nécessaire.
Supposons (1). Alors:
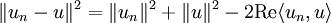
Par convergence faible de (un)n:
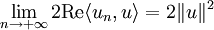
et donc par (1) (un)n tend vers u dans H.

















































