Inégalité de Cauchy-Schwarz - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, l'inégalité de Cauchy-Schwarz, aussi appelée inégalité de Schwarz, ou encore inégalité de Cauchy-Bunyakovski-Schwarz, se rencontre dans de nombreux domaines tels que l'algèbre linéaire, l'analyse avec les séries et en intégration.
Cette inégalité s'applique dans le cas d'un espace vectoriel sur le corps des nombres réels ou complexes muni d'un produit scalaire. Dans le cas complexe, le produit scalaire désigne une forme hermitienne définie positive. Son contexte général est donc celui d'un espace préhilbertien.
Cette inégalité possède de nombreuses applications, comme le fait d'établir l'inégalité triangulaire montrant que la racine carrée de la forme quadratique associée au produit scalaire est une norme, ou encore que le produit scalaire est continu. Elle fournit des justifications ou des éclairages dans des théories où le contexte préhilbertien n'est pas central.
Elle doit son nom à Hermann Amandus Schwarz et à Augustin Louis Cauchy.
Énoncé
Le théorème s'énonce couramment de la façon suivante :
Théorème 1 — Soit
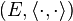
De plus, les deux membres sont égaux si et seulement si x et y sont linéairement dépendants.
Conséquences et applications
Conséquences
L'inégalité de Cauchy-Schwarz a des applications importantes. Elle permet notamment de montrer que l'application

Elle permet également de définir l'angle non orienté entre deux vecteurs non nuls d'un espace préhilbertien réel, par la formule :
Dans le cas de l'espace euclidien
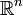
Dans le cas des fonctions à valeurs complexes de carré intégrable, elle s'écrit
-

Cette inégalité est un cas particulier des inégalités de Hölder.
Autres applications
- L'inégalité de Cauchy-Schwarz est aussi un outil fondamental de l'analyse dans les espaces de Hilbert. Grâce à elle, on peut construire une injection du préhilbert E dans son dual topologique : pour tout vecteur y, la forme linéaire qui à x associe <x,y> est continue, de norme égale à celle de y. Ceci permet d'énoncer le théorème de représentation de Riesz selon lequel si E est un espace de Hilbert alors cette injection est un isomorphisme.
On la retrouve aussi dans le théorème de Lax-Milgram.
- Cependant ses applications peuvent sortir du cadre strict de l'analyse dans les espaces de Hilbert. En effet elle se retrouve parmi les ingrédients utiles à l'inégalité de Paley-Zygmund en théorie des probabilités et du traitement du signal.
En théorie des probabilités toujours, dans l'espace des variables aléatoires admettant un moment d'ordre 2, l'inégalité de Cauchy-Schwarz fournit l'inégalité
- En optimisation, le cas d'égalité dans l'inégalité de Cauchy-Schwarz appliquée à la dérivée directionnelle permet de justifier que le gradient donne la direction de plus grande pente.
- En physique, l'inégalité de Cauchy-Schwarz joue un rôle important dans le principe d'incertitude d'Heisenberg et a pris place dans le débat sur l'hypothèse des quanta de lumière. Elle serait utilisée en informatique quantique.




















































