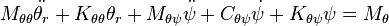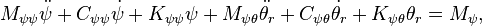Dynamique des cycles - Définition

Theory

Although its equations of motion can be linearized, a bike is a nonlinear system. The variable(s) to be solved for cannot be written as a linear sum of independent components, i.e. its behavior is not expressible as a sum of the behaviors of its descriptors. Generally, nonlinear systems are difficult to solve and are much less understandable than linear systems.

In the idealized case, in which friction and any flexing is ignored, a bike is a conservative system. Damping, however, can still be demonstrated: side-to-side oscillations will decrease with time. Energy added with a sideways jolt to a bike running straight and upright (demonstrating ) is converted into increased forward speed, not lost, as the oscillations die out.

A bike is a nonholonomic system because its outcome is path-dependent. In order to know its exact configuration, especially location, it is necessary to know not only the configuration of its parts, but also their histories: how they have moved over time. This complicates mathematical analysis.

Finally, in the language of control theory, a bike exhibits non-minimum phase behavior. It turns in the direction opposite of how it is initially steered, as described above in the section on

Degrees of freedom

The number of degrees of freedom of a bike depends on the particular model being used. The simplest model that captures the key dynamic features, four rigid bodies with knife edge wheels rolling on a flat smooth surface, has 7 degrees of freedom (configuration variables required to completely describe the location and orientation of all 4 bodies):

1. x coordinate of rear wheel contact point
2. y coordinate of rear wheel contact point
3. orientation angle of rear frame (yaw)
4. rotation angle of rear wheel
5. rotation angle of front wheel
6. lean angle of rear frame (roll)
7. steering angle between rear frame and front end

Adding complexity to the model, such as suspension, tire compliance, frame flex, or rider movement, adds degrees of freedom. While the rear frame does pitch with leaning and steering, the pitch angle is completely constrained by the requirement for both wheels to remain on the ground, and so can be calculated geometrically from the other seven variables. If the location of the bike and the rotation of the wheels are ignored, the first five degrees of freedom can also be ignored, and the bike can be described by just two variables: lean angle and steer angle.

Equations of motion

The equations of motion of an idealized bike, consisting of

• a rigid frame,
• a rigid fork,
• two knife-edged, rigid wheels,
• all connected with frictionless bearings and rolling without friction or slip on a smooth horizontal surface and
• operating at or near the upright and straight-ahead, unstable equilibrium

can be represented by a single fourth-order linearized ordinary differential equation or two coupled second-order differential equations, the lean equation

and the steer equation

where

• θ_r is the lean angle of the rear assembly,
• ψ is the steer angle of the front assembly relative to the rear assembly and
• M_θ and M_ψ are the moments (torques) applied at the rear assembly and the steering axis, respectively. For the analysis of an uncontrolled bike, both are taken to be zero.

These can be represented in matrix form as where

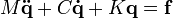
• M is the symmetrical mass matrix which contains terms that include only the mass and geometry of the bike,
• C is the so-called damping matrix, even though an idealized bike has no dissipation, which contains terms that include the forward speed V and is asymmetric,
• K is the so-called stiffness matrix which contains terms that include the gravitational constant g and V² and is symmetric in g and asymmetric in V²,
• is a vector of lean angle and steer angle, and
• is a vector of external forces, the moments mentioned above.

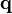
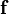
In this idealized and linearized model, there are many geometric parameters (wheelbase, head angle, mass of each body, wheel radius, etc.), but only four significant variables: lean angle, lean rate, steer angle, and steer rate. These equations have been verified by comparison with multiple numeric models derived completely independently.

Eigenvalues

It is possible to calculate eigenvalues, one for each of the four state variables (lean angle, lean rate, steer angle, and steer rate), from the linearized equations in order to analyze the normal modes and self-stability of a particular bike design. In the plot to the right, eigenvalues of one particular bicycle are calculated for forward speeds of 0–10 m/s (22 mph). When the real parts of all eigenvalues (shown in dark blue) are negative, the bike is self-stable. When the imaginary parts of any eigenvalues (shown in cyan) are non-zero, the bike exhibits oscillation.

There are three forward speeds that can be identified in the plot to the right at which the motion of the bike changes qualitatively:

1. The forward speed at which oscillations begin, at about 1 m/s (2.2 mph) in this example, sometimes called the double root speed due to there being a repeated root to the characteristic polynomial (two of the four eigenvalues have exactly the same value). Below this speed, the bike simply falls over as an inverted pendulum does.
2. The forward speed at which oscillations do not increase, where the weave mode eigenvalues switch from positive to negative in a Hopf bifurcation at about 5.3 m/s (12 mph) in this example, is called the weave speed. Below this speed, oscillations increase until the uncontrolled bike falls over. Above this speed, oscillations eventually die out.
3. The forward speed at which non-oscillatory leaning increases, where the capsize mode eigenvalues switch from negative to positive in a pitchfork bifurcation at about 8.0 m/s (18 mph) in this example, is called the capsize speed. Above this speed, this non-oscillating lean eventually causes the uncontrolled bike to fall over.

Between these last two speeds, if they both exist, is a range of forward speeds at which the particular bike design is self-stable. In the case of the bike whose eigenvalues are shown here, the self-stable range is 5.3–8.0 m/s (12–18 mph). The fourth eigenvalue, which is usually stable (very negative), represents the castoring behavior of the front wheel, as it tends to turn towards the direction in which the bike is traveling. Note that this idealized model does not exhibit the and instabilities described above. They are seen in models that incorporate tire interaction with the ground or other degrees of freedom.

Experimentation with real bikes has so far confirmed the weave mode predicted by the eigenvalues. It was found that tire slip and frame flex are not important for the lateral dynamics of the bicycle in the speed range up to 6 m/s.

The idealized bike model used to calculate the eigenvalues shown here does not incorporate any of the torques that real tires can generate, and so tire interaction with the pavement cannot prevent the capsize mode from become unstable at high speeds, as Wilson and Cossalter suggest happens in the real world.