Effet Shklovski - Définition

Ordre de grandeur et mise en évidence

Un pulsar ordinaire est animé d'une vitesse typique de 1 000 km/s et situé à une distance typique de l'ordre de quelques kiloparsecs, l'application numérique donne

.

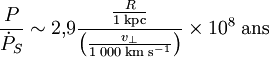
En pratique, un pulsar voit sa rotation ralentir au cours du temps (voir Ralentissement des pulsars), du fait qu'il dissipe de l'énergie électromagnétique du fait de sa rotation, et que cette perte d'énergie est compensée par une perte d'énergie cinétique de rotation. La période réelle d'un pulsar décroît donc au cours du temps d'une quantité . Cette quantité permet de calculer l'âge caractéristique t_c d'un pulsar, qui correspond sous certaines hypothèses (voir Âge caractéristique), à l'âge réel du pulsar. L'âge caractéristique est donné par

.

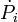
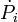
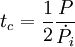
En pratique, on observe la combinaison du ralentissement apparent dû à l'effet Schklovski et du ralentissement intrinsèque du pulsar, qu'il n'est pas possible de distinguer par la seule observation du ralentissement (réel et apparent) du pulsar. Ainsi, l'âge caractéristique mesuré t_m est-il

,

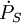
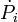
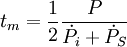
que l'on peut réécrire en

.

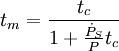
En pratique, l'effet Schkolvski bruite la mesure de l'âge caractéristique, mais n'est gênante que dans les cas où l'âge caractéristique est de l'ordre de ou plus grand que l'ordre de grandeur donné ci-dessus. L'effet n'est donc gênant que pour les pulsars suffisamment âgés, ce qui concerne essentiellement les pulsars millisecondes.

L'effet Shklovski peut toutefois être distingué du ralentissement intrinsèque si l'on parvient à mesurer la vitesse transverse du pulsar et sa distance. La distance peut être mesurée soit directement par parallaxe ou parallaxe chronométrique, soit indirectement par la mesure de dispersion ou l'absorption HI. La vitesse se déduit alors par la mesure du mouvement propre du pulsar, c'est-à-dire son déplacement sur la sphère céleste. Dans les deux cas, il est préférable que le pulsar soit proche, de façon à ce que les effets de parallaxe et le mouvement propre soient importants. Pour le pulsar PSR B1133+16, il a ainsi pu être mis en évidence que l'effet Shklovski était responsable de 5 % environ du ralentissement observé. Il est possible que pour des pulsars millisecondes, il soit la contribution dominante de celui-ci.

Une autre situation où l'effet Shklovski est plus facile à mettre en évidence est celui où la période du phénomène observé n'a pas de raison de varier au cours du temps. C'est par exemple le cas pour la période orbitale d'un système binaire. Celle-ci peut être amenée à décroître du fait de l'émission de rayonnement gravitationnel (comme pour le pulsar binaire PSR B1913+16), mais une augmentation de celle-ci peut révéler l'effet Shklovski à l'œuvre. PSR J0437-4715, un pulsar binaire, est le premier dont les paramètres ont pu être mesurés avec suffisamment de précision pour qu'il eût pu être établi que le ralentissement de sa période orbitale était entièrement due à l'effet Shklovski.