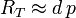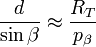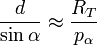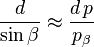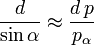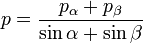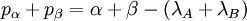Parallaxe - Définition

Introduction

Figure 1 : Un exemple simplifié de parallaxe

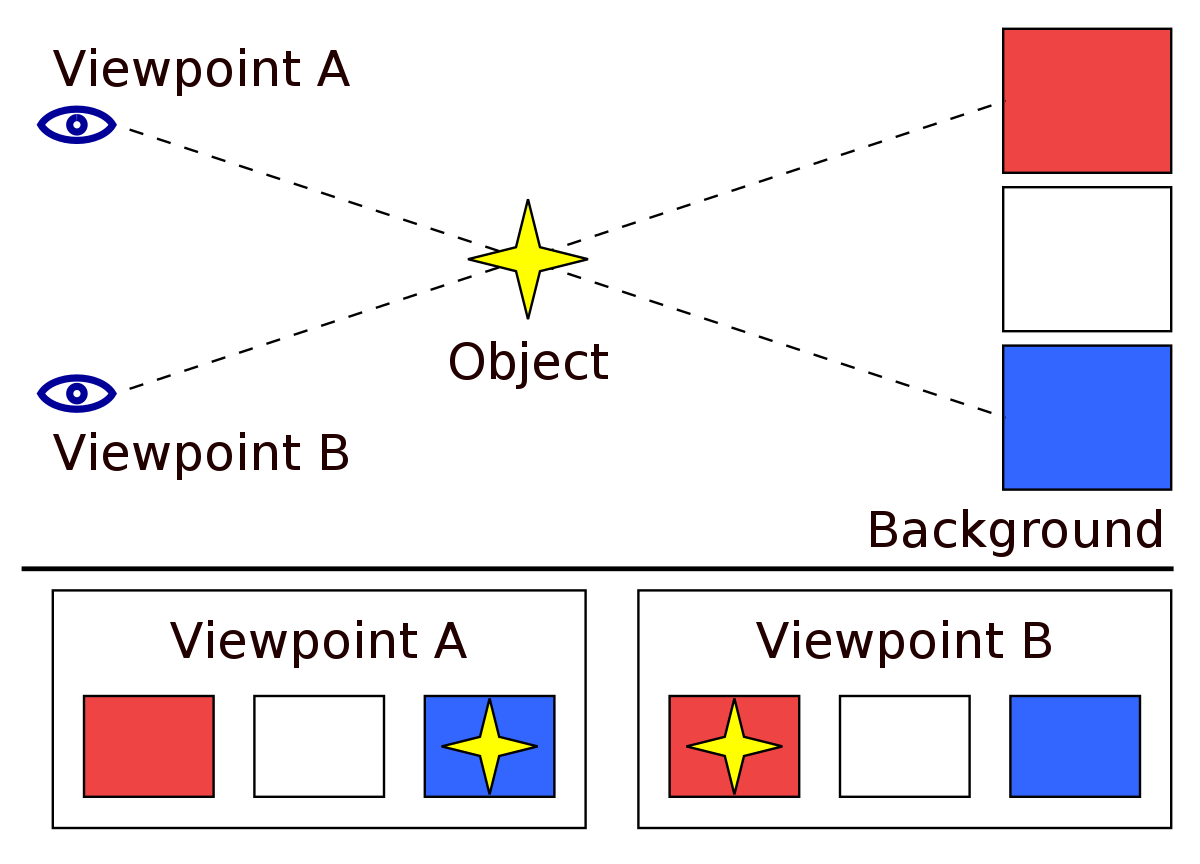
La parallaxe est l’incidence du changement de position de l’observateur sur l’observation d’un objet. En d'autres termes, la parallaxe est l'impact (ou l'effet) de changement de position de l'observateur sur un objet observé.

Ce mot apparaît au XVI^e siècle, emprunté au grec παράλλαξις, qui signifie « déplacement contigu ; parallaxe ».

Métrologie

L’erreur de parallaxe est l’angle entre la direction du regard d’un observateur et la perpendiculaire à la graduation d’un appareil de mesure, amenant à une erreur de lecture de la mesure effectuée.

Afin de supprimer pratiquement cette erreur, l’observateur doit se placer de manière à confondre l’aiguille ou l’index avec l’image qu’en donne un miroir situé en arrière plan.

Photographie

Parallaxe entre le viseur et l’objectif

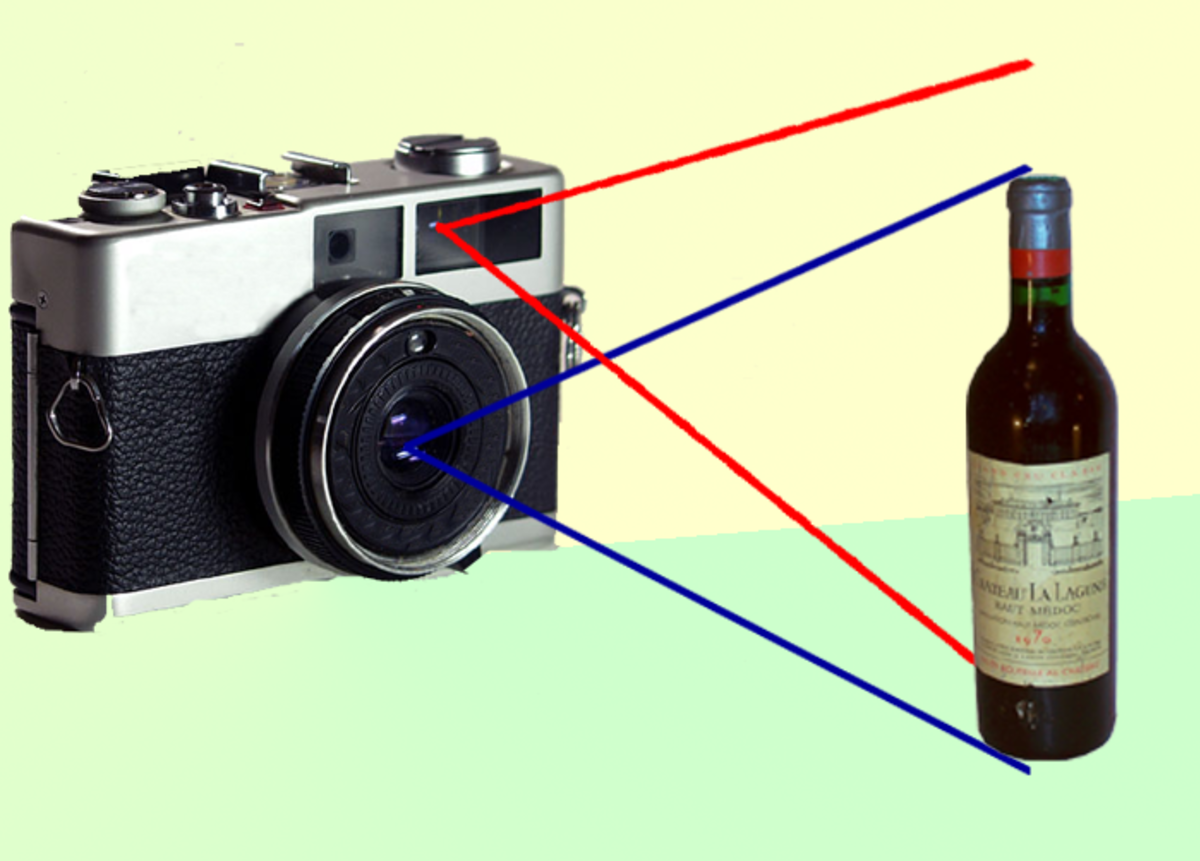
La parallaxe de visée est la différence de cadrage entre l’image donnée par un viseur et l’image passant dans l’objectif d’un appareil photographique. Un appareil photographique bi-objectif est un appareil dans lequel la visée est effectuée à travers un objectif situé au-dessus de l’objectif de prise de vue. L’imprécision due à la parallaxe n’existe bien sûr pas avec un appareil photographique reflex mono-objectif (dont la visée se fait à travers la lentille de prise de vue grâce à un miroir).

Psychologie

En psychologie, la parallaxe est une modification de la subjectivité, la différence de perception d’une même réalité.

On dit d’un sujet qu’il fait une parallaxe lorsqu’il arrive à percevoir une réalité ou un état dans un sens différent, et qu’il parvient à se décentrer de sa propre perception pour construire un nouveau sens de cette même réalité. L’essence même de la thérapie psychologique consiste à aider le sujet à se créer une parallaxe de la réalité qui allie le sens commun et sa sérénité.

Astronomie

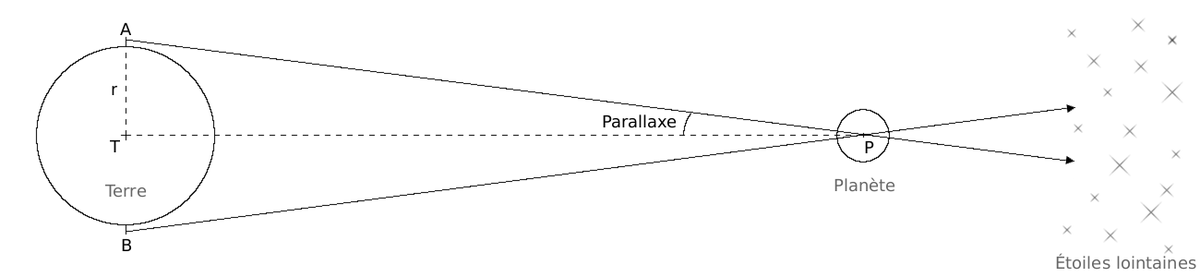
En astronomie, la parallaxe est l’angle sous lequel peut être vue depuis un astre une longueur de référence :

• pour les astres du système solaire, c’est le rayon de la Terre qui a été choisi ; il s’agit de la parallaxe diurne ;
• pour les astres extérieurs au système solaire, la référence est le demi-grand axe de l’orbite terrestre, soit une unité astronomique ; il s’agit de la parallaxe annuelle.

La détermination de la parallaxe lunaire (entre 52' et 62'), est due à Nicolas-Louis de Lacaille et à Joseph Jérôme Lefrançois de Lalande (1732-1807), opérant simultanément en deux points de la surface de la Terre très éloignés l’un de l’autre.

On confond l’arc et la tangente

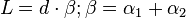
mesurés par les observateurs O1 et O2 distant de L

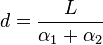
Plus l’astre considéré est proche, plus son changement apparent de direction lié au déplacement de l’observateur est important. Les astronomes du XVIII^e siècle et du début du XVIII^e ont longuement cherché à mettre en évidence cet effet géométrique à titre de confirmation du système héliocentrique de Copernic. La première mesure de la parallaxe d’une étoile a été publiée en 1838 par l’allemand Friedrich Wilhelm Bessel.

Parallaxe diurne

On appelle parallaxe diurne d’un astre l’angle sous lequel on verrait depuis cet astre le rayon terrestre (r) aboutissant au lieu d’observation (A). Cet angle est négligeable pour les étoiles. En revanche, c’est de lui qu’il s’agit quand on parle de la parallaxe d’un astre du système solaire.

Lorsque l’astre est à l’horizon du lieu (en A), cet angle atteint un maximum, la parallaxe horizontale. Cette dernière atteint elle-même sa valeur maximale pour un lieu situé à l’équateur, la parallaxe horizontale équatoriale. Par exemple, la parallaxe horizontale équatoriale du Soleil vaut 8,794″. Le rapport de la parallaxe horizontale équatoriale moyenne du Soleil et de la parallaxe horizontale d’un astre fournit une valeur approchée de la distance d’un astre du système solaire, en unités astronomiques.

Parallaxe diurne : deux observateurs se placent en deux points A et B de la Terre les plus éloignés possible et notent la configuration des étoiles entourant l’astre observé. Ils peuvent ainsi calculer les angles BAP et ABP, puis en déduire la parallaxe qui permettra d’obtenir la distance TP.

Parallaxe annuelle

On appelle parallaxe annuelle d’une étoile l’angle sous lequel on verrait depuis cette étoile (E) le demi-grand axe de l’orbite terrestre (R).

Mesure de distance des astres par la parallaxe annuelle

La parallaxe annuelle des plus proches étoiles permet d’en calculer la distance, cette distance étant proportionnelle à la cotangente de l’angle de parallaxe, soit approximativement l’inverse de cet angle ; entre la distance D de l’étoile au Soleil — exprimée en unités astronomiques — et la valeur θ de sa parallaxe annuelle — exprimée en radians — existe la relation θ = 1 / D.

Friedrich Wilhelm Bessel utilisa cette méthode pour la première fois en 1838 pour la binaire 61 du Cygne.

Avec l’usage de cette méthode de mesure de distance, une unité de longueur spécifique fut définie : le parsec, qui est la distance d’un astre dont la parallaxe annuelle est d’une seconde d’arc (toutes les parallaxes annuelles sont inférieures à la seconde d’arc - la fraction ¹⁄₃₆₀₀ d’un degré -, et sont habituellement exprimées en millisecondes d’arc).

Cette unité facilite les calculs ; par exemple, pour Proxima Centauri, l’étoile la plus proche du Système solaire, la parallaxe est de 760 millisecondes, ce qui correspond à une distance est de ¹⁄_0,760 = 1,32 pc.

À la fin des années 1980, les parallaxes annuelles d’environ 8 000 étoiles avaient été obtenues à partir de mesures directes (parallaxes trigonométriques), les mesures effectuées à partir des instruments construits à la surface de la Terre étant affectés d’imprécisions liées aux perturbations atmosphériques.

Grâce au satellite d’astrométrie européen Hipparcos, les parallaxes annuelles d’environ 100 000 étoiles sont maintenant connues avec une précision de 0,001″.

Parallaxe spectroscopique

Un certain nombre de parallaxes d’étoiles plus lointaines sont déterminées par l’analyse spectroscopique de leur rayonnement. Cette analyse spectrale permet d’estimer leur magnitude absolue, et donc leur distance à partir de leur magnitude apparente ; cette méthode est désignée par parallaxe spectroscopique ou parallaxe photométrique.

Ces dénominations ne sont que des abus de langage, cette méthode imprécise n’ayant aucun rapport avec celles décrites précédemment (pour les étoiles proches, des différences de l’ordre de 20 % entre parallaxe trigonométrique et parallaxe spectroscopique ne sont pas rares).

La parallaxe dans le débat héliocentrisme/géocentrisme

Dans le procès de Galilée, l’Inquisiteur St Robert Bellarmin (mort au moment du procès de 1633) fit l’objection que, si la Terre se mouvait, on devrait observer une parallaxe (selon la définition ci-dessus). Mais aucune parallaxe n’ayant été mesurée, ce fait devenait un argument contre l’héliocentrisme. Galilée répondit que les étoiles étaient trop lointaines pour que la parallaxe puisse être vue et mesurée avec les instruments d’alors.

Tycho Brahe avait également employé cet argument en faveur de l’immobilité de la Terre. Il avait fait sur l’éloignement des plus proches étoiles une hypothèse très en dessous de la réalité, qui en fait confirme l’argument de Galilée.

La parallaxe mesurée par Bessel correspond à celle prévisible en admettant la théorie héliocentrique. La présentation de la parallaxe comme une preuve de l’héliocentrisme signifie qu’on suppose que les mouvements des autres étoiles par rapport au Soleil comme négligeables devant les mouvements des objets du système solaire.

Méthode de Lalande et La Caille

Tous deux sur le même méridien, Lalande se plaça à Berlin et La Caille au Cap. Ils calculèrent une parallaxe de 57 minutes et 11 secondes d’arc. Voyons comment.

On appelle d la distance TL séparant le centre de la Terre du centre de la Lune. Dans le triangle TML rectangle en M, on écrira

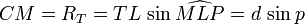
Comme , on peut considérer que p est un très petit angle, d’où l’approximation

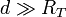
	(éq. 1)

Appliquons le théorème des sinus :

• dans le triangle TBL : d’où

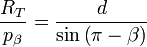
(éq. 2a)

en considérant p_β petit

• dans le triangle TAL : d’où

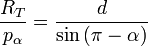
(éq. 2b)

en considérant p_α petit

Relions maintenant p_α et p_β à p : on insère pour cela l’équation (1) dans les équations (2a) et (2b)

(2a) donne

(éq. 3)

(2a) donne

(éq. 4)

On déduit par addition de (3) et (4) une expression de p,

(éq. 5)

Travaillons maintenant sur les sommes des angles

• dans le triangle TBL :
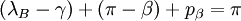
• dans le triangle TAL :

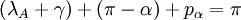
En ajoutant ces deux relations, il vient

(éq. 6)

Introduisons ce résultat dans l’expression (5) :

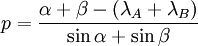
On obtient ainsi l’expression de la parallaxe en fonction des mesures angulaires effectuées aux lieux A et B (visées et latitudes).

D’après la mesure effectuée par Lalande (Berlin, λ_B = 53,52^oN) et La Caille (Le Cap, λ_A = 34,66^oS), p = 53′11″, il vient d’après l’expression (1)

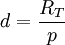
Avec la rayon terrestre moyen et p en radians, nous obtenons

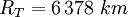
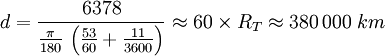
Le résultat obtenu est tout à fait cohérent. Les dernières mesures de parallaxe réalisées au laser par la NASA ont donné une parallaxe de 57 minutes et 20 secondes d’arc, valeur très proche de celle déterminée par Lalande et La Caille en 1751.

Pour réinvestir les calculs : parallaxe solaire 8,8″ - déterminer la distance Terre-Soleil !