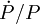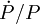Effet Shklovski - Définition

Introduction

En astronomie, l'effet Shklovski est le nom donné à la variation de la période apparente d'un pulsar du simple fait de son déplacement dans l'espace, à l'image d'un effet Doppler-Fizeau qui voit la fréquence du son émis par une source varier quand celle-ci passe devant l'observateur. En pratique, la variation de la période du signal émis par un pulsar peut être interprétée comme étant due à une variation de vitesse de celui-ci, c'est-à-dire une accélération. Pour cette raison, le terme d'accélération séculaire est parfois utilisé en lieu et place d'effet Shklovsky, donnée en l'honneur de l'astronome russe I. S. Shklovsky qui l'a mis en évidence en 1970.

Calcul de l'effet Shklovski

L'effet Shklovski n'est rien d'autre que le calcul classique de l'effet Doppler en tenant compte du déplacement de la source d'un signal périodique. Il prédit que l'on mesure une variation apparente de la période P du signal émis par un pulsar donnée par

,

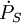
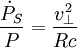
où R est la distance du pulsar, c la vitesse de la lumière et la norme de la composante de la vitesse perpendiculaire à la direction dans laquelle se trouve le pulsar.

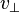
Soit P₀ la période du signal du pulsar. La période apparente P mesurée par un observateur situé à l'origine du système de coordonnées s'écrit :

.

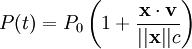
La dérivée de cette quantité, notée par un point se calcule immédiatement en

,

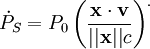
ce qui donne, en développant

,

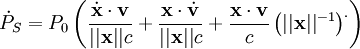
c'est-à-dire

,

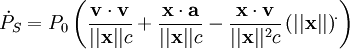
a étant l'accélération du pulsar. En notant avec l'indice la composante des vecteur le long de la ligne de visée et R la distance , il vient

,

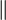
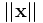
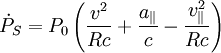
puisque la quantité représente la variation de la distance du pulsar, c'est-à-dire la composante de sa vitesse radiale .

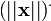
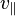
Dans le cas où le pulsar est en mouvement rectiligne uniforme, son accélération est nulle, et il reste, en notant le module de la composante transverse de la vitesse ( ),

.

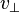
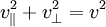
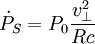
En supposant que la vitesse du pulsar est petite devant la vitesse de la lumière, l'on peut approximer la période P(t) par P₀, d'où finalement

.

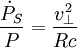
Dans le cas où le pulsar subit une accélération, alors il faut tenir compte du terme en a dans la dérivation. L'on sait que la partie radiale de l'accélération, , est donnée par (voir Coordonnées polaires en analyse vectorielle)

,

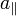
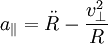
d'où on déduit la formule générale

.

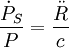
Même dans le cas où l'accélération est nulle, cette formule reste valable. En effet, le fait que la vitesse du pulsar soit constante ne signifie pas que sa distance à l'observateur croisse linéairement avec le temps. Si l'on note R_m la distance minimale d'approche du pulsar que l'on suppose animé d'une vitesse constante v, alors sa distance R à l'observateur évolue selon

.

Cette fonction tend vers une fonction linéaire du temps à grand t Dans ce cas là, la trajectoire du pulsar est quasiment radiale, et on n'observe quasiment pas de variation de période, mais la quantité est toujours non nulle (et toujours positive).

 

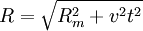
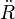
Accélération des pulsars

La formule exacte de l'effet Shklovski est en réalité (voir démonstration ci-dessus)

,

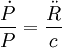
où intervient la dérivée seconde de la distance R au pulsar. Quand le pulsar ne se déplace pas le long de la ligne de visée, un mouvement rectiligne uniforme donne lieu à une dérivée seconde de la distance. Cependant, il est aussi possible que cette dérivée seconde soit non nulle si le pulsar accélère. Celle-ci peut du reste être explicitement être mise en évidence si le pulsar accélère vers l'observateur, auquel cas la quantité est négative, et ne peut correspondre à un ralentissement intrinsèque. Ceci se produit pour des pulsars situés dans des puits de potentiel marqués comme des amas globulaires, quand le pulsar est approximativement situé dans l'alignement de l'observateur et du centre du puits, et derrière celui-ci. Ces conditions sont réunies pour les deux pulsars PSR B2127+11A et PSR B2127+11D situés dans l'amas M15 qui présentent chacun un de l'ordre de -2,0×10^-16 s^-1.