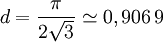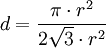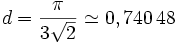Empilement compact - Définition

Introduction

L'empilement compact est la manière d'agencer des sphères dans l'espace afin d'avoir la plus grande densité de sphères, sans que celles-ci ne se recouvrent.

C'est un problème que l'on se pose en général en géométrie euclidienne dans l'espace à trois dimensions, mais on peut aussi le généraliser au plan euclidien (les « sphères » étant alors des cercles), dans un espace euclidien à n dimensions (n > 3), avec des hypersphères, ou dans un espace non-euclidien.

Arrangement compact de cercles dans un plan

Arrangement de rondelles d'agrumes

Arrangement en quinconce d'un plan compact

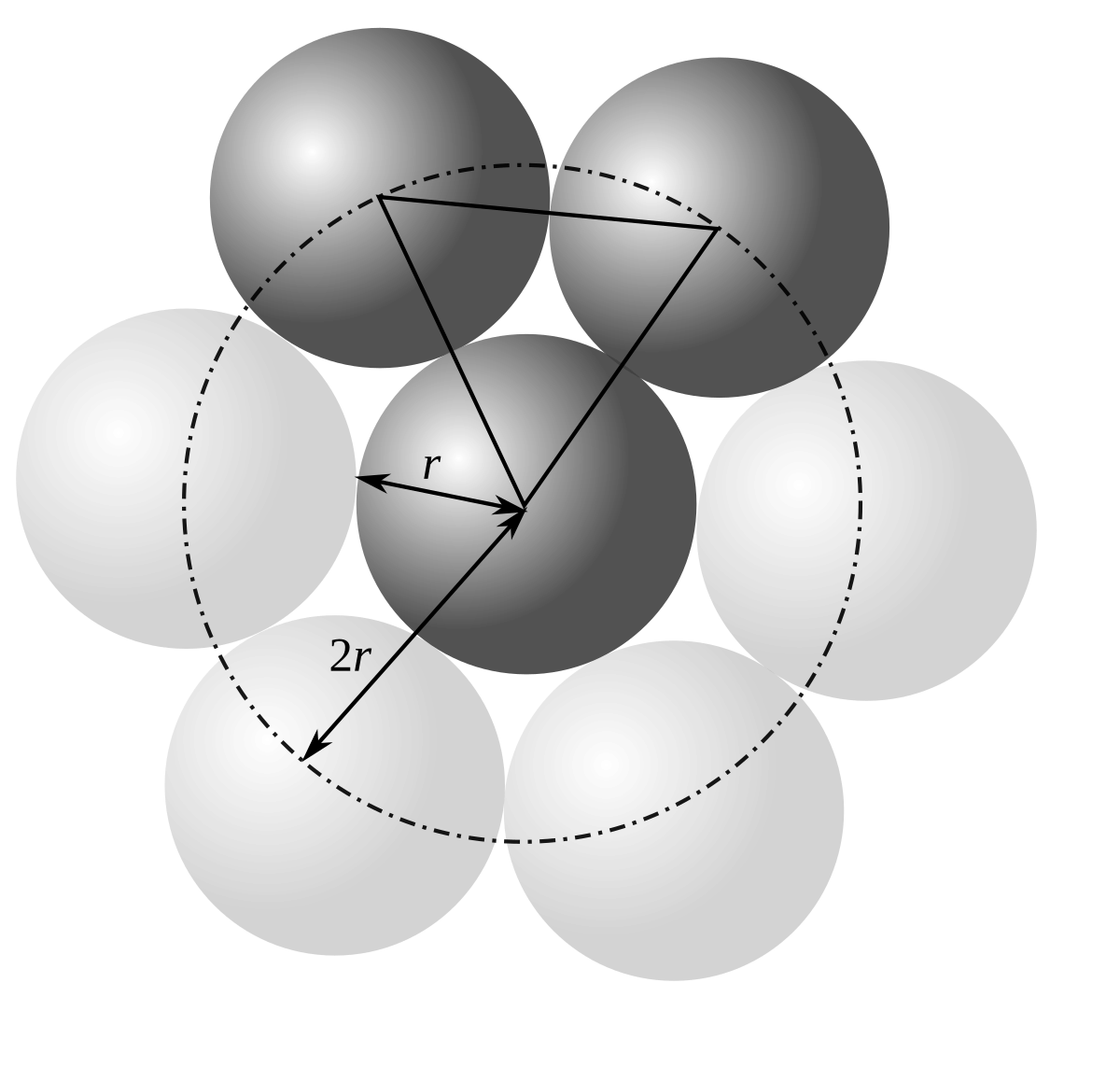
Sur un plan, on peut disposer au maximum six cercles de rayon r autour d'un cercle de même rayon. Les centres de trois cercles en contact définissent un triangle équilatéral puisqu'ils sont distants de 2r les uns des autres. Chaque angle valant 60° (π/3), on peut mettre ainsi 6 triangles avec un sommet en commun pour former un hexagone régulier.

On peut constater aisément que c'est l'organisation la plus compacte qui soit en rangeant des billes de même volume dans une enceinte de taille appropriée.

Carl Friedrich Gauss prouva qu'aucun arrangement régulier n'est plus dense. Tel n'est pas le cas lorsque les sphères n'ont pas la même taille (voir l'arrangement de rondelles d'agrumes).

La densité surfacique de cet arrangement est

Calcul

Considérons quatre cercles en contact deux à deux. Les centres de ces cercles forment un losange de côté 2r. On peut ainsi découper le plan en un pavage de losanges définissant un réseau.

Chaque losange comprend deux portions de disques de 2π/3 et deux portions de disques de π/3. La somme des aires de ces portions de disques est donc égale à la surface d'un disque, soit πr².

Le losange lui-même a pour aire . Les disques occupent donc une proportion de surface égale à

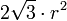
Dimensions plus élevées

Dans les espaces euclidiens de dimension supérieure à 3, le problème d'empilement compact se généralise aux hypersphères. Les densités des arrangements réguliers les plus compacts sont connues jusqu'en dimension 8, et pour la dimension 24 (voir l'article constante d'Hermite).

Asymptotiquement, la densité d_n de l'arrangement le plus compact (régulier ou non) décroît exponentiellement en fonction de la dimension n. Il n'y a pas de raison de penser que les arrangements les plus denses soient réguliers en général. Néanmoins le meilleur encadrement connu sur d_n est la même dans les deux cas : .

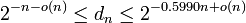
Empilement compact de sphères

empilement compact de 35 sphères

deux manières d'empiler trois plans compacts

Considérons trois sphères en contact sur un plan (plan A). On peut placer une quatrième sphère posée sur le creux entre les trois premières, les centres des sphères formant un tétraèdre régulier.

En positionnant ainsi des sphères dans les creux du plan compact A, on obtient un deuxième plan compact (plan B). Gauss montra que cette organisation était l'organisation régulière ayant la plus grande densité. En 1611, Johannes Kepler conjectura que c'était l'arrangement spatial le plus compact. Cette conjecture n'a toujours pas été prouvée, mais selon les travaux de Thomas Hales et Andrew Mellon à l'Université de Pittsburgh en 1998, cette conjecture est une quasi certitude.

Lorsque l'on ajoute un troisième plan, on peut mettre les sphères soit en correspondance avec celles du premier plan (plan A), soit dans une troisième possibilité de placement définissant un nouveau plan compact (plan C).

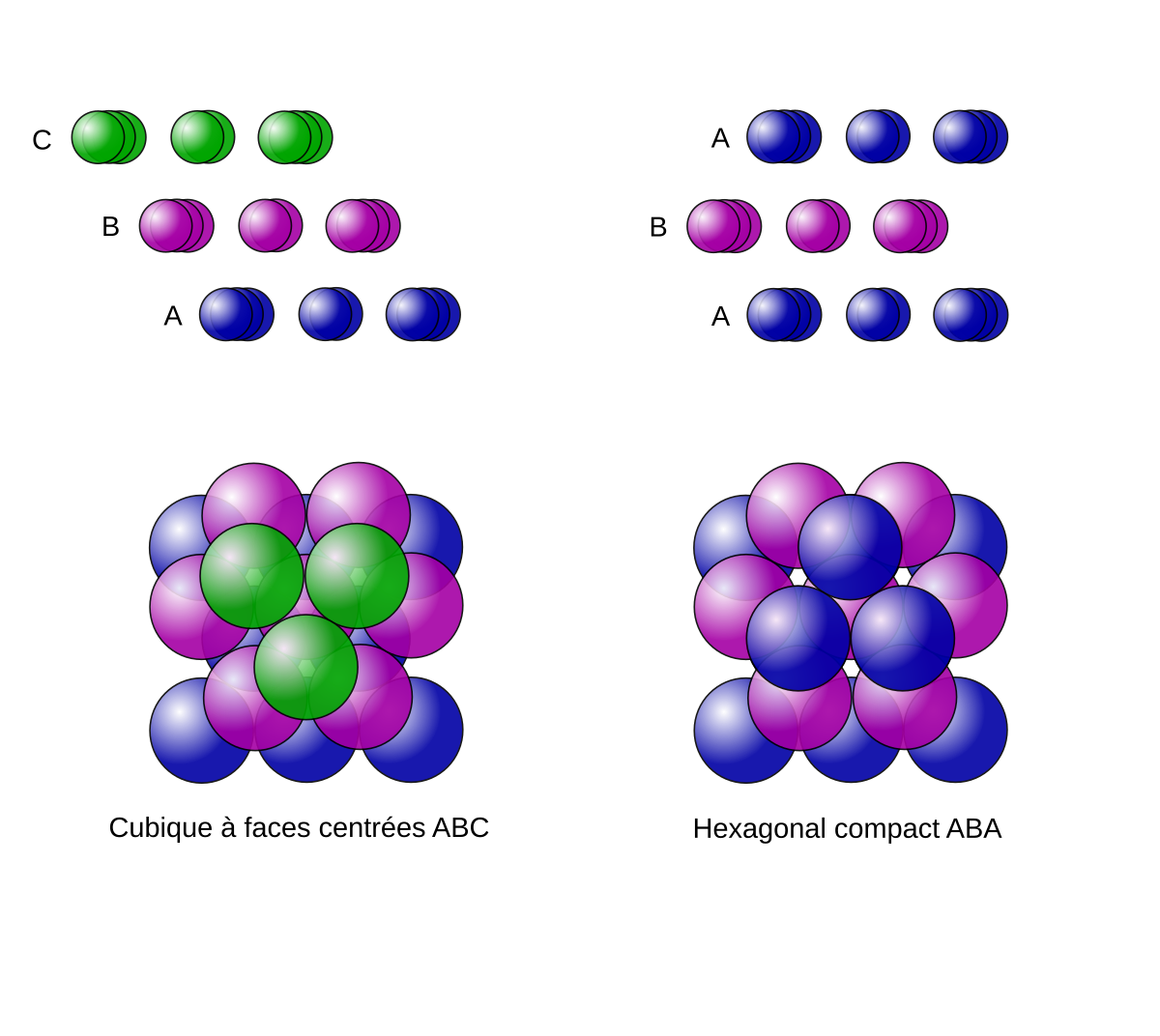
Il existe ainsi trois types de plans compacts A, B et C qui peuvent en se combinant engendrer une infinité de types d'empilements compacts :

• A-B-A-B… empilement dit « hexagonal compact » ;
• A-B-C-A-B-C… empilement dit « cubique à faces centrées » ;
• A-B-A-C-A-B-A-C… ;
• A-B-C-B-A-B-C-B… ;
• …

Quel que soit l'arrangement, chaque sphère est entourée de 12 autres sphères, et la densité volumique vaut dans tous les cas :

Calcul

Le calcul peut se faire de manière simple sur un empilement cubique à faces centrées et sur un empilement hexagonal compact (voir le lien externe pour le calcul de la compacité). Pour les autres empilements compacts, il suffit de découper la structure en groupes de trois plans pour se retrouver dans l'un des cas précités.