Géométrie euclidienne - Définition

Introduction

Euclide.

La géométrie euclidienne commence avec les Éléments d'Euclide, qui est à la fois une somme des connaissances géométriques de l'époque et une tentative de formalisation mathématique de ces connaissances. Les notions de droite, de plan, de longueur, d'aire y sont exposées et forment le support des cours de géométrie élémentaire. La conception de la géométrie est intimement liée à la vision de l'espace physique ambiant au sens classique du terme.

Les conceptions géométriques connaissent, depuis les travaux d'Euclide, des évolutions suivant trois axes principaux :

1. Pour vérifier les critères de rigueur logique actuels, la définition axiomatique subit de profonds changements, l'objet mathématique restant néanmoins le même.
2. Pour ne plus se limiter aux dimensions deux et trois et pour permettre l'élaboration d'une théorie plus puissante, un modèle algébrique de la géométrie est envisagé. L'espace euclidien est maintenant défini comme un espace vectoriel ou affine réel de dimension finie muni d'un produit scalaire.
3. Enfin, la structure géométrique euclidienne n'est plus la seule envisageable ; il est établi qu'il existe d'autres géométries cohérentes.

Plus de 2000 ans après sa naissance, l'espace géométrique euclidien est un outil toujours efficace aux vastes domaines d'applications. Par exemple, l'espace des physiciens reste encore principalement du domaine de la géométrie euclidienne, l'astronomie étant l'exception la plus notoire.

Son aspect mathématique est traité de manière didactique dans l'article produit scalaire. L'article se fonde sur la formalisation d'un vecteur à l'aide d'un bipoint, développé dans vecteur. Une approche plus poussée, fondée sur la formalisation axiomatique de l'espace vectoriel est développée dans espace euclidien.

L’approche euclidienne de la science de l’espace

La géométrie euclidienne au sens des antiques traités du plan et de l'espace ; elle est souvent présentée comme une géométrie « de la règle et du compas ». Les objets considérés sont les points, les segments, les droites, les demi-droites, avec leurs propriétés d'incidence (la règle), ainsi que les cercles (le compas). Les enjeux essentiels sont l'étude de figures et la mesure.

Les outils de la géométrie d'Euclide

La construction d'Euclide se fonde sur cinq postulats :

1. Un segment de droite peut être tracé en joignant deux points quelconques distincts.
2. Un segment de droite peut être prolongé indéfiniment en une ligne droite.
3. Étant donné un segment de droite quelconque, un cercle peut être tracé en prenant ce segment comme rayon et l'une de ses extrémités comme centre.
4. Tous les angles droits sont congruents.
5. Si deux lignes sont sécantes avec une troisième de telle façon que la somme des angles intérieurs d'un côté est strictement inférieure à deux angles droits, alors ces deux lignes sont forcément sécantes de ce côté.

Les raisonnements sur les figures géométriques portent sur leurs intersections et leurs dimensions : sur l'incidence et la mesure. De ce point de vue, certaines transformations des figures sont utiles ; les plus pertinentes sont les similitudes, c'est-à-dire les transformations qui conservent les rapports des distances. Les similitudes les plus simples sont les rotations, les symétries, les translations, qui conservent les distances, ainsi que les homothéties. À partir de ces quelques objets de base, toutes les similitudes peuvent être construites par composition.

La construction d'Euclide permet le développement des notions de mesure de longueur, d'aire, de volume, d'angle. Il existe de nombreuses aires de surfaces usuelles calculables par les techniques des Éléments. Une méthode, la méthode d'exhaustion qui préfigure l'intégration, permet d'aller plus loin. Archimède , par exemple réalise la quadrature de la parabole. Une limite de la notion de mesure vient de ce que les nombres considérés sont seulement les nombres constructibles (à la règle et au compas).

Les deux théorèmes fondamentaux sont le théorème de Pythagore et celui de Thalès. Un peu d'analyse permet d'aller plus loin avec la trigonométrie. C'est le premier exemple de construction d'un pont entre la géométrie euclidienne pure et une autre branche mathématique, pour enrichir la palette d'outils disponibles.

Approche géométrique de l'algèbre

La formule de l'aire d'un rectangle ou d'un triangle, le théorème de Thalès ainsi que celui de Pythagore offrent tous des relations algébriques entre des grandeurs que sont les côtés d'un triangle ou d'un rectangle. Ces différentes méthodes sont l'un des ingrédients de l'algèbre naissante, initiée par Diophante, et développée par la civilisation arabe.

Le traité d'Al-Khawarizmi, un mathématicien persan du VIII^e siècle, intitulé La transposition et la réduction a pour objectif la résolution d'une équation du second degré quelconque. Sa méthode se fonde sur ce que l'on appelle maintenant les identités remarquables, qui, chez lui se démontrent toutes à l'aide de la géométrie euclidienne.

Cette géométrisation de l'algèbre porte ses fruits aussi en arithmétique, la science des nombres. La première démonstration montrant l'existence de grandeurs irrationnels est probablement géométrique. Certains calculs comme la valeur du n^ième nombre triangulaire ou encore la somme des n premiers cubes d'entiers sont réalisés géométriquement.

Succès et limites

Figure à la règle et au compas : heptadécagone, un polygone régulier de 17 côtés.

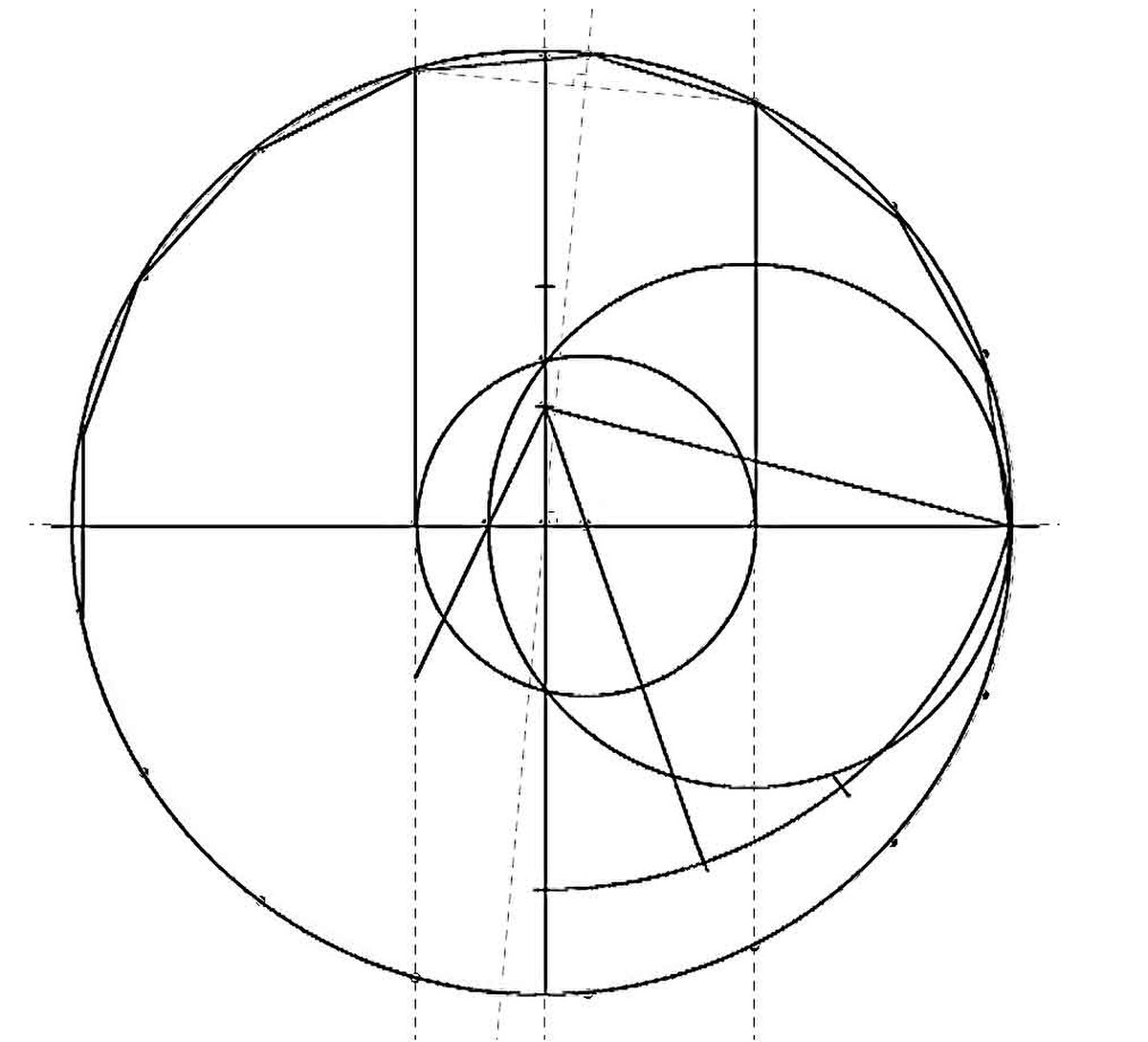
Un objectif de la géométrie euclidienne est la construction de figures à la règle et au compas. L'étude du triangle relève de ce domaine. La richesse des résultats obtenus est illustrée par la liste des éléments remarquables d'un triangle. Une famille de figures emblématiques est celle des polygones réguliers (voir l'article Partage d'une tarte). Ils ne sont cependant pas tous constructibles. Les techniques de construction s'appliquent non seulement au plan, mais aussi à l'espace comme le montre l'étude des polyèdres.

Une spécificité de la géométrie euclidienne réside dans le fait qu'elle n'utilise initialement que peu ou pas du tout de théorèmes complexes et puissants d'algèbre ou d'analyse. C'est une mathématique autonome et indépendante, où les preuves proviennent essentiellement de raisonnements purement géométriques. Cependant, pour les cas complexes, comme la construction de la figure ci-contre, d'autres outils, par exemple les polynômes, se révèlent indispensables (cf Théorème de Gauss-Wantzel). Les trois grands problèmes de l'antiquité, à savoir la quadrature du cercle, la trisection de l'angle et la duplication du cube, à l'aide seulement de la règle et du compas, ne se sont d'ailleurs montrés possibles qu'avec l'apport d'une autre branche des mathématiques : l'arithmétique, algébrique ou analytique.

La géométrie euclidienne a de nombreuses applications. La Renaissance fait largement appel aux techniques des Éléments. L'architecture, la peinture à travers la perspective regorgent d'exemples de cette nature. L'art des entrelacs de Léonard de Vinci est un autre cas d'utilisation. Ces mathématiques servent aussi à la mesure, à la fois pour les arpenteurs et dans un objectif scientifique. Elles permettent à Ératosthène de mesurer la circonférence de la Terre. Les techniques utilisées, dites de triangulation et ayant pour base la trigonométrie, permettent aux marins de connaître leur position.

Application et nouveaux outils : espace euclidien et physique

Système solaire (tailles et distances relatives non à l'échelle).

À partir du XVI^e siècle les mathématiques s'éloignent de plus en plus de la géométrie du triangle. La géométrie euclidienne garde son utilité car elle modélise avec pertinence le monde physique ambiant.

Cependant, l'approche purement antique devient trop restrictive. Elle n'offre pas un cadre suffisant pour le développement des mathématiques. Pour étudier les coniques Blaise Pascal utilise un nouvel outil : le repère. Il s'avère précieux à la naissance du calcul infinitésimal. Avec le temps l'algèbre et l'analyse deviennent prédominantes : de nouvelles techniques, éloignées de celles héritées d'Euclide, sont développées. En ce qui concerne la modélisation de l'espace physique, ces nouveautés sont utilisées dans le cadre d'une géométrie peu formalisée, néanmoins avec un large succès. Les théories datant d'avant le XX^e siècle se contentent de ce cadre. Encore maintenant, et dans un contexte très général, la géométrie usuelle de la physique reste euclidienne. Elle permet des résultats spectaculaires, comme la mécanique newtonienne.

Ce n'est qu'en 1915, qu'une autre géométrie, celle de la relativité générale, explique mieux un phénomène, celui de l'avance du périhélie de Mercure. La géométrie euclidienne reste maintenant valable à trois exceptions près :

• les distances astronomiques, dans le cadre de la relativité générale ;
• les vitesses proches de la lumière, avec la géométrie de la relativité restreinte ;
• les dimensions inférieures à la taille des particules, dans le cadre de certaines théories contemporaines comme les supercordes.

Si la modélisation de la géométrie de l'espace reste souvent la même que celle de l'Antiquité (aux exceptions déjà citées près), la formalisation change radicalement.