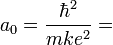Énergie d'ionisation - Définition
La liste des auteurs de cet article est disponible ici.
L'énergie d'ionisation en mécanique quantique
Le modèle de Bohr n'est pas tout à fait conforme à la théorie de la mécanique quantique, mieux décrite par le Modèle de Schrödinger selon laquelle la localisation de l'électron est décrite non pas de façon déterministe, mais comme un "nuage" de localisations dotées d'une certaine probabilité d'être plus ou moins près du noyau. Cette approche plus rigoureuse est également un peu plus compliquée, mais on peut donner quelques pistes pour l'aborder : Le nuage correspond à une fonction d'onde ou, plus précisément à une combinaison linéaire des déterminants de Slater, c'est-à-dire, selon le Principe d'exclusion de Pauli, des produits antisymétriques des Orbitale atomique ou des Orbitale moléculaire. Cette combinaison linéaire est un développement en interaction de configurations de la fonction d'onde électronique.
Dans le cas général, pour calculer la nième énergie d'ionisation, il faut soustraire l'énergie d'un système de Z − n + 1 électrons d'un système de Z − n électrons. Le calcul de ces énergies n'est pas simple, mais il s'agit d'un problème assez classique en chimie numérique. En première approximation, l'énergie d'ionisation peut être déduite du théorème de Koopmans
L'approche simple de Feynman
L'inconvénient de l'approche semi-classique, qui fait l'hypothèse implicite d'un électron en orbite autour du noyau, avec la force centrifuge qui s'oppose à la force d'attraction, à l'instar d'un satellite en orbite est qu'il est avéré depuis le début du XXe siècle qu'elle est erronée : un électron en orbite ne manquerait pas de rayonner, et s'effondrerait sur le noyau suivant une trajectoire en spirale. Feynman a montré qu'il n'était pas nécessaire de faire cette hypothèse pour estimer le rayon du noyau d'hydrogène. Il fait tout de même appel à l'hypothèse d'une trajectoire circulaire (d'où l'expression du moment cinétique L=mvr) et à la quantification de ce moment cinétique selon Bohr.
En rappelant que l'énergie totale du système noyau + électron est
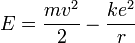
et en utilisant la quantification de Bohr
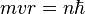
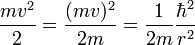
on obtient
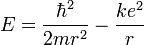
"Nous ne savons pas ce que vaut a0, mais nous savons que l'atome va s'arranger pour faire une sorte de compromis de façon que son énergie soit aussi petite que possible", écrit Feynman dans son célèbre "Lectures on Physics"
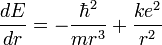
En écrivant que la valeur de cette dérivée est nulle au point r = a0, on obtient la valeur de a0