Spirale - Définition

Introduction

La spirale est une forme fréquente dans le monde animal et végétal, chez les gastéropodes par exemple

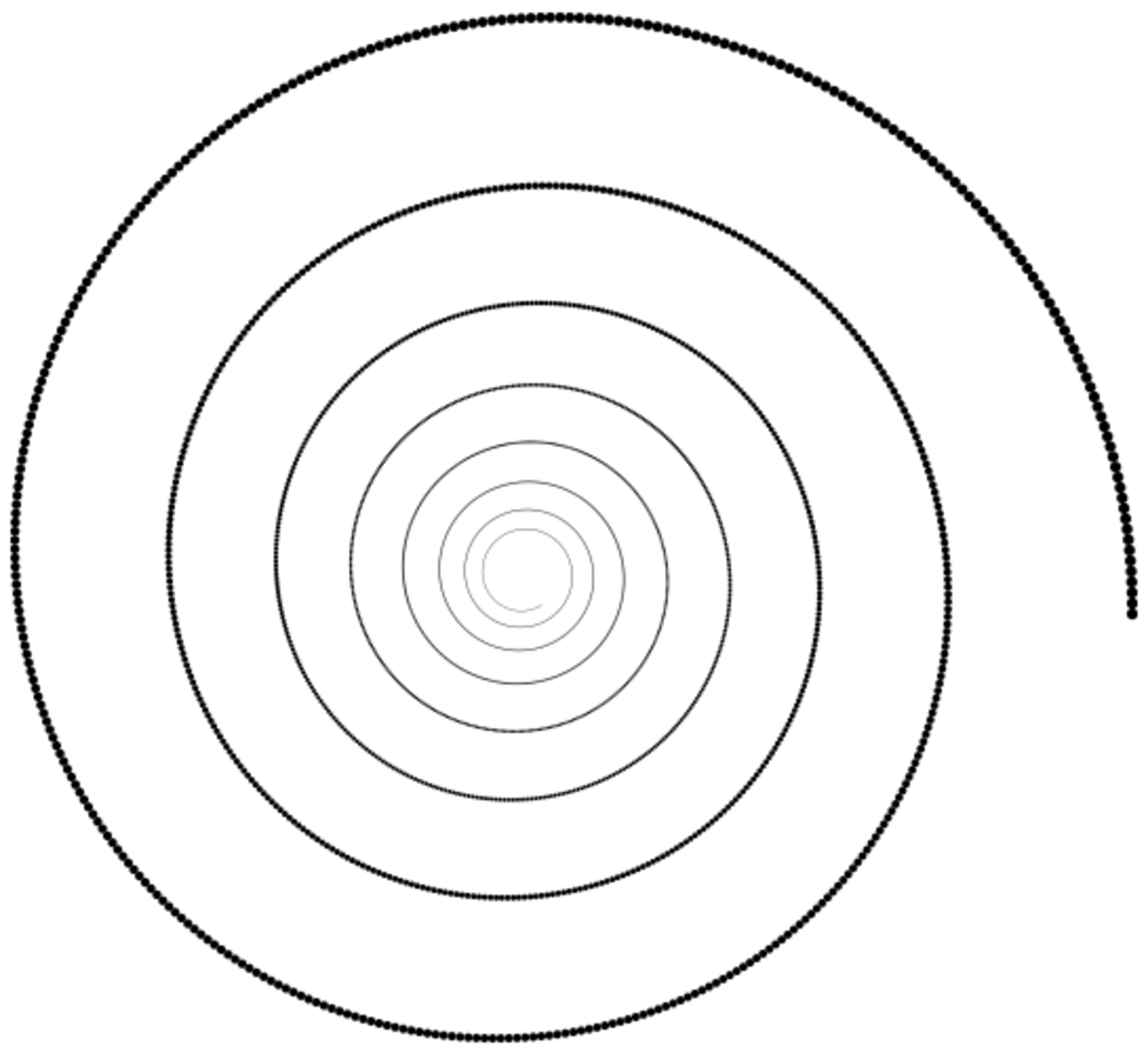
En mathématiques, une spirale est une courbe qui commence en un point central puis s'en éloigne de plus en plus, en même temps qu'elle tourne autour.

Le terme spirale se réfère en général à une courbe plane. Lorsqu'une spirale se développe en trois dimensions, on parle plutôt d'hélice.

Étymologie

La spirale est un des motifs qui semblent avoir fasciné l'homme depuis la préhistoire, des gravures celtes aux tatouages polynésiens

Escaliers formant une spirale

En latin spira ou en grec speira, ce mot désigne un enroulement.

Dans le langage courant, et notamment en dessin et en architecture les adjectifs spiral et spiralé désignent toutes les formes évoquant la spirale mathématique (escalier en spirale...) ou comprenant une suite de circonvolutions.

Spirales à centres multiples

L'éloignement progressif d'une spirale dépend du nombre des centres qui ont servi à la former. Il y a des spirales :

• à 2 centres qui sont situés sur une même ligne,
• à 3 centres qui sont situés aux trois sommets d'un triangle équilatéral,
• à 4 centres qui sont situés aux quatre sommets des angles d'un carré.

Spirales à deux dimensions

Une spirale à deux dimensions se décrit facilement à l'aide de coordonnées polaires : le rayon r est donné par une fonction continue et monotone de l'angle θ. Le cercle en est alors un cas dégénéré.

Il existe plusieurs types de spirales à deux dimensions. Voici les plus importantes :

• La spirale d'Archimède :
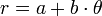
• La spirale hyperbolique :
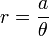
• La spirale logarithmique :
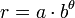
• La spirale de Fermat :
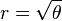
• La spirale de Nielsen
• La spirale de Cotes
• La spirale de Galilée
• La spirale de Fibonacci : cas particulier de la spirale logarithmique construite avec une suite de Fibonacci

Une spirale a nécessairement une infinité de spires distinctes; le rayon polaire peut croître indéfiniment avec l'angle, ou tendre vers une limite finie; dans ce dernier cas, la spirale est asymptote à un cercle et même parfois à une droite (spirale hyperbolique).

Exemples

Spirale triple, constituant la figure du triskel des celtes.

Mouvement contraint de 2 spirales d'Archimède l'une dans l'autre, qui évoque schématiquement le principe de certaines pompes. Le point de contact entre les 2 spirales se déplace lui-même en suivant le dessin de la spirale rouge.

En botanique, la spirale est présente dans la disposition des graine du tournesol, ou dans le point d'insertion des feuilles sur la tige (l'angle dièdre passant par l'axe de la tige et deux points qui se succèdent est la divergence, valeur caractéristiques de l'espèce).

Culture

• la spirale est un motif fréquent dans la décoration (frises, bijoux, tissus, dessins, tatouages, carrelages, etc)
• Regarder une spirale qui tourne provoque un effet d'optique, qui fascine et est réputé faciliter l'hypnose. C'est un thème souvent exploité dans les dessins animés.
• En bande dessinée, les yeux d'un personnage dessinés en spirale évoquent - selon le contexte - la confusion du personnage, le fait qu'il soit sonné, fou, etc.

Construction

Un procédé simple permet de tracer d'un mouvement continu une spirale relativement régulière, par exemple pour la décoration de jardins : Il suffit d'enrouler un cordeau attaché à un piquet planté au centre désigné de la spirale. En déroulant ensuite le cordeau autour du piquet en le gardant tendu, une pointe maintenue verticale et attachée au bout de ce cordeau permet de tracer au sol une spirale au fur à mesure que le cordeau se déroule. Dans ce procédé, les spires de la ligne tracée sont évidemment d'autant plus écartées, que le piquet central est plus gros. On obtient une (approximation de) développante du cercle

Construction d'une fausse spirale (ou spirale approximative) sur une feuille de papier

Avec un compas et une règle :

1. Tracer une droite qui partage la feuille en deux parties égales.
2. Placer deux points A₁ et A₂ sur la droite aux environs du centre de la feuille. La distance entre le point A₁ et le point A₂ paramètre la concentration de la courbe. Plus cette distance est courte, plus la spirale sera concentrée.
3. Piquer le compas sur le point A₁. L'écarter de la distance A₁A₂.
4. Tracer le demi-cercle d'origine A₂. Noter A₃ le point issu de l'intersection entre le demi-cercle et notre droite.
5. Piquer le compas sur le point A₂. L'écarter de la distance A₂A₃.
6. Tracer le demi-cercle d'origine A₃. Noter A₄ le point issu de l'intersection entre le demi-cercle et notre droite.
7. Piquer le compas sur le point A₃. L'écarter de la distance A₃A₄.
8. Tracer le demi-cercle d'origine A₄. Noter A₅ le point issu de l'intersection entre le demi-cercle et notre droite.
9. etc.

Le résultat est une spirale construite à partir de demi-cercles dont le rayon augmente de la distance A₁A₂ à chaque fois.

Plusieurs variantes sont possibles et combinables :

• le rayon de chaque demi-cercle n'est pas augmenté d'une valeur constante, mais double ;
• tracer des quarts de cercles au lieu de demi-cercles (nécessite deux droites perpendiculaires). Ou des tiers de cercles, avec un triangle équilatéral qui détermine trois demi-droites.