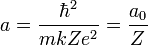Énergie d'ionisation - Définition

Introduction

Le potentiel d'ionisation ou énergie d'ionisation d'un atome ou d'une molécule est l'énergie qu' il faut fournir à un atome neutre pour arracher un électron. Plus généralement, la nième énergie d'ionisation est l'énergie requise pour arracher le nième électron après que les n − 1 premiers électrons ont été arrachés. En chimie physique, le concept d'énergie d'ionisation est l'opposé de celui d'affinité électronique, c'est-à-dire de sa propension à céder ou au contraire à retenir un électron.

La réaction d'ionisation de l'atome A s'écrit :

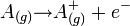
Généralités

L'énergie d'ionisation s'exprime en eV ou en Joule ou en kiloJoule/mole (kJ/mol). (1 électron-Volt égale 96,485 kJ/mol). C'est une grandeur qui est toujours positive, ce qui signifie qu'il faut toujours fournir de l'énergie à un atome pour lui arracher un (ou plusieurs) électrons. L'énergie d'ionisation varie en fonction de l'atome ou de la molécule considérée, ainsi que de son état d'ionisation.

On peut ioniser un atome possédant plus d'un électron en plusieurs étapes. Par exemple, un atome de bore possède cinq électrons : deux dans une couche interne (1s²) et trois dans la couche de valence(2s² et 2p¹). L'énergie d'ionisation d'ordre n est l'énergie nécessaire pour séparer successivement n électrons de l'atome. L'énergie de première ionisation varie beaucoup selon les atomes. L'énergie d'ionisation augmente le long d'une ligne de la table périodique des éléments puis diminue brusquement lorsque l'on passe à une autre ligne.

L'électron arraché que l'on considère dans le concept d'énergie d'ionisation provient de la couche de valence. Mais il peut se faire qu'un électron des couches profondes de l'atome soit arraché sans que les électrons des couches superficielles l'aient été préalablement; dans ce cas les électrons se réorganisent ensuite, donnant lieu à un rayonnement (fluorescence X).

Interprétation électrostatique et modèle semi-classique

L'énergie d'ionisation atomique peut être calculée à partir du Potentiel électrique et du modèle de Bohr d'un atome.

On considère un électron, de charge -e et un ion avec une charge +Ne, où N est le nombre d'électrons manquant à l'ion. Selon le modèle de Bohr, si l'électron s'approchait, il pourrait rester lié à l'atome sur une orbite d'un certain rayon a. Le potentiel électrostatique V à la distance a du noyau considéré comme ponctuel s'écrit, avec  :

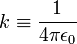
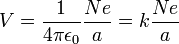
étant entendu que le potentiel, défini à une constante près, est choisi nul pour une distance a infinie.

L'énergie électrostatique d'un électron placé à la distance a dans le potentiel du noyau ci-dessus est donnée par :

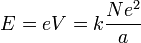
On fait l'hypothèse qu'il s'agit de l'énergie d'ionisation, également appelée potentiel d'ionisation (par abus de langage, puisqu'il s'agit d'une énergie potentielle (en joules) et non du potentiel (en volts) ci-dessus. En fait, ces grandeurs sont proportionnelles, avec un facteur toujours égal à la charge de l'électron, d'où la tolérance à cet abus).

À ce stade de l'approche classique, l'analyse est encore incomplète puisque la distance a reste inconnue. Il convient alors d'associer à chaque électron d'un élément chimique donné une distance caractéristique choisie de telle sorte que l'expression du potentiel d'ionisation soit en accord avec des données expérimentales.

Procédons maintenant au calcul de cette distance caractéristique en utilisant une approche semi-classique basée sur l'hypothèse de Bohr, qui étend le modèle classique en quantifiant la quantité de mouvement (première quantification de Bohr). Cette approche est très bien vérifiée pour l'atome d'hydrogène qui n'a qu'un seul électron, et dont le noyau est réduit à un proton. La norme du moment cinétique orbital pour une orbite circulaire est quantifiée selon Bohr :

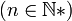
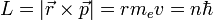
L'énergie totale de l'électron est la somme de ses énergies potentielle U et cinétique T, c'est-à-dire :

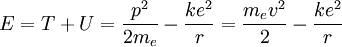
La vitesse peut être éliminée du terme correspondant à l'énergie cinétique en posant que l'attraction coulombienne doit être compensée par la force centrifuge :

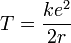
Ce qui permet alors d'exprimer l'énergie en fonction de k, e, et r.

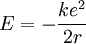
La quantification de la quantité de mouvement exprimée quelques lignes plus haut selon l'hypothèse de Bohr permet alors d'écrire :

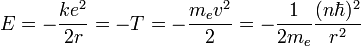
d'où

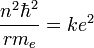
D'où l'on tire la relation entre n et r :

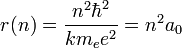
On appelle rayon de Bohr a₀ le rayon de la première orbite, n=1. Le calcul numérique donne :

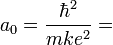
On peut alors exprimer l'équation de l'énergie en faisant appel au rayon de Bohr :

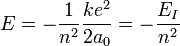
où après calculs, on trouve la valeur de l'énergie d'ionisation de l'atome d'hydrogène dans son état fondamental (n=1)

On peut étendre ce modèle aux ions hydrogénoïdes de numéro atomique Z, atomes ayant perdu (Z-1) électrons et qui ne possèdent, à l'instar de l'hydrogène, qu'un seul électron. Le e² des formules ci-dessus était apparu en faisant le produit de la charge du noyau d'hydrogène +e et de la charge de l'électron -e. Maintenant la charge du noyau est +Ze, on remplace donc e² par Ze² et, pour une raison similaire (voir le calcul de a ci-dessous), a₀ par a₀ / Z dans les formules. L'énergie de "dernière ionisation" serait donc :

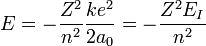
et la distance a cherchée au début de cette section :

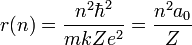
donne, pour n=1 :