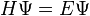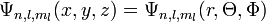Orbitale atomique - Définition

Introduction

Le terme d’orbitale atomique est une notion de physique quantique, utilisée dans le modèle quantique de l’atome. Ainsi dans ce modèle, contrairement à l’ancien modèle planétaire de l’atome, on ne considère plus que les électrons d’un atome sont en orbite circulaire (ou même elliptique) autour du noyau, mais occupent de manière probabiliste certaines régions de l’espace autour du noyau.

On définit alors comme orbitale atomique une zone de l’espace où la probabilité de trouver un électron autour du noyau est de 95%. Une orbitale peut ne pas être connexe.

Définition

Une orbitale atomique indique la probabilité de présence d'un électron autour du noyau d'un atome isolé. Elle dépend de la fonction d'onde de l'électron (et plus précisément de son module au carré), déterminée par l'équation de Schrödinger en utilisant l'approximation orbitale.

La fonction d'onde satisfait l'équation aux valeurs propres de l'hamiltonien (appelée aussi « équation de Schrödinger indépendante du temps », ou encore « équation des états stationnaires »):

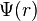
H est un opérateur appelé hamiltonien, est la fonction d'onde et E est l'énergie associée à cette fonction d'onde. La fonction d'onde peut être écrite soit en coordonnées cartésiennes x,y et z, soit en coordonnées sphériques r, et  :

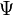
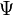
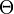
où

• indique la probabilité de trouver l'électron dans l'élément de volume centré en
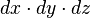
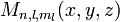
• Ψ² est la densité volumique de probabilité de présence, ou densité électronique.

Nombres quantiques

L’état d’un électron dans un atome est fonction de quatre paramètres discrets qui sont des nombres quantiques. Le principe d'exclusion de Pauli (issu du modèle ondulatoire de l’électron) interdit à deux électrons au sein d’un atome d’avoir le même quadruplet de nombres quantiques.

Parmi ces quatre paramètres les indices n, l et m_l sont les trois nombres quantiques décrivant une orbitale atomique de l’électron ; ce sont des entiers sans dimension, dont la combinaison avec le numéro atomique du noyau permet de définir le niveau d’énergie de l’électron dans cet état quantique :

• le nombre quantique principal :
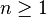
• le nombre quantique secondaire (ou azimutal) :
• le nombre quantique tertiaire (ou magnétique) :

Enfin le quatrième nombre quantique, le spin, est noté s ou m_s. Le spin est une grandeur homogène à un moment angulaire qui peut être comprise comme la « révolution » de l’électron sur lui-même (ce qui n’est qu'une image dans la mesure où l’électron est considéré comme essentiellement ponctuel si on le considère comme une particule avec un probabilité de présence, mais distribué dans l’espace si on le considère comme la superposition de ses fonctions d’onde qui lui conférent son niveau quantifié d’énergie dans l’orbitale) : deux valeurs sont possibles (spin positif +½ et spin négatif −½) ce qui concrètement signifie que deux électrons, au plus, peuvent occuper une orbitale atomique donnée. Si deux électrons occupent une orbitale, l’un aura un spin positif, l’autre un spin négatif.

Le nombre quantique secondaire (ou azimutal) l définit la forme et la symétrie de l’orbitale, et peut être noté en utilisant les lettres s, p, d, f :

• l = 0 correspond à une orbitale s (sharp ou simple) ;
• l = 1 correspond à une orbitale p (principal) ;
• l = 2 correspond à une orbitale d (diffuse) ;
• l = 3 correspond à une orbitale f (fundamental) ;
• les types d’orbitales suivants éventuels sont notés g, h, i, j.

Les nombres quantiques principal et secondaire (ou azimutal) définissent ce que l’on appelle une sous-couche électronique que l'on note souvent en accolant la valeur numérique de n et la lettre associée à l. Quelques exemples :

• l'orbitale de paramètres n = 1 et l = 0 forme la sous-couche électronique 1s ;
• l'orbitale de paramètres n = 2 et l = 0 forme la sous-couche électronique 2s ;
• les orbitales de paramètres n = 2 et l = 1 forment la sous-couche électronique 2p ;
• etc.

On note couramment en exposant, après l'indication de la sous-couche, le nombre d’électrons occupant cette sous-couche. Le nombre maximum d’électrons (toujours pair) pour chacune des sous-couches ne dépend que des valeurs possible du nombre quantique tertiairem_l, lesquelles sont limitées uniquement par le nombre quantique secondaire (azimutal) l ; il augmente de 4 pour chaque sous-couche, selon la formule . Ainsi :

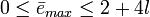
• pour l = 0 au maximum 2 électrons occupe la sous-couche : ns² ;
• pour l = 1 au maximum 6 électrons occupe la sous-couche : np⁶ ;
• pour l = 2 au maximum 10 électrons occupe la sous-couche : nd¹⁰ ;
• pour l = 3 au maximum 14 électrons occupe la sous-couche : nf¹⁴ ;
• etc.

On note également parfois en indice, après l'indication de la sous-couche, le nombre total d’électrons occupant les sous-couches de niveau d’énergie inférieur ou égal à celui de cette sous-couche (comme on peut le voir dans le diagramme suivant et dans des tables d’orbitales en général). Dans l’état fondamental de l’atome (non excité, hors ionisation et hors liaison covalente dans une molécule), ce nombre correspond au numéro atomique de l’élément.

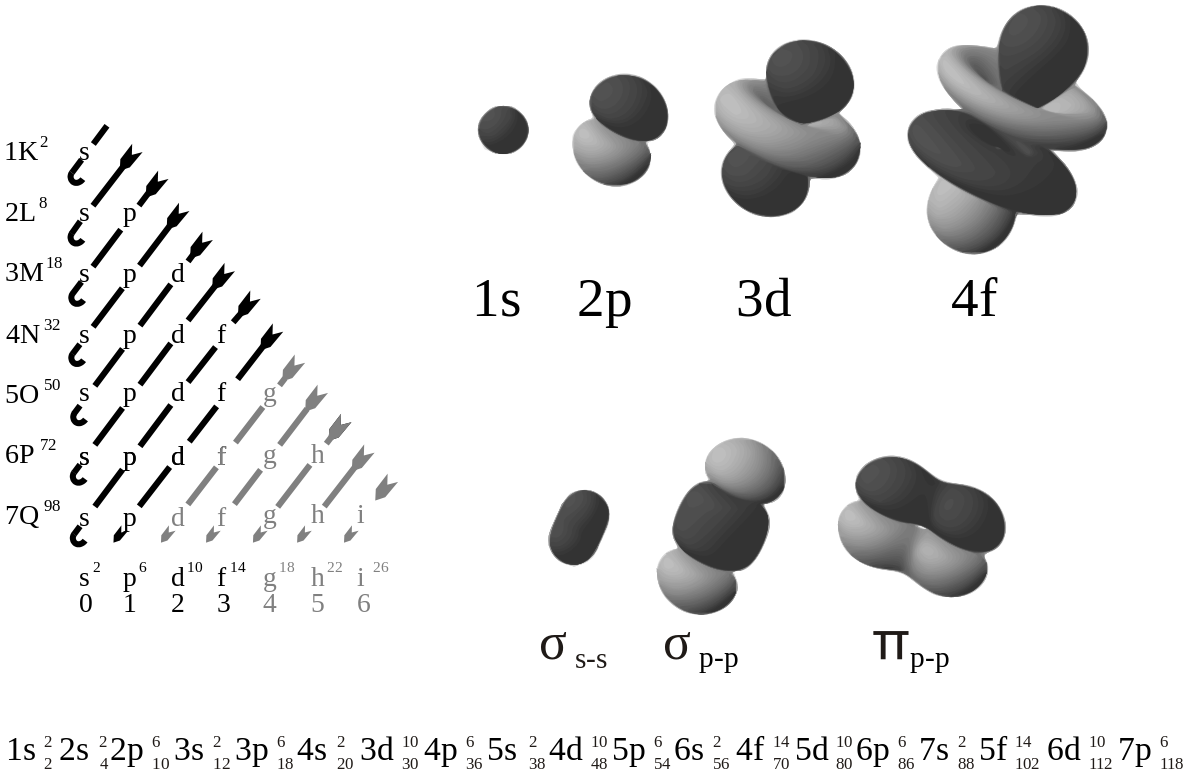
Table d’orbitales

Orbitales électroniques.

Le diagramme ci-dessus représentant des orbitales électroniques aux niveaux atomique et moléculaire :

• le tableau à gauche présente les orbitales arrangées par niveau croissant d’énergie selon la règle de Madelung : dans l’état fondamental de l’atome ou de l’ion, les électrons occupent les orbitales de niveau d’énergie le plus faible en premier, en les remplissant paire par paire, du moins tant que l’atome n’est pas dans un état excité (auquel cas un électron peut gagner un niveau des niveaux d'énergie plus élevés) ;
• les orbitales électroniques de l’atome sont fonction de trois paramètres : deux angles et la distance du noyau, r (qui dépend du numéro atomique N et du premier nombre quantique n de l’orbitale) ;
• les images à droite respectent l’angle de l’orbitale, mais ne représentent pas complètement les orbitales (qui sont en fait chacune distribuées spatialement mais représentées dans les limites de l’espace qu’elles occupent à 95 % d’énergie) ; de plus elles ne sont pas représentées à la même échelle (le paramètre r est ignoré dans cette représentation)
• leur forme n’est valable que si l’électron ne forme pas de liaison covalente avec un autre atome dans une molécule, auquel cas les orbitales de la paire covalente changent de forme et ne sont plus centrées sur le noyau atomique (la figure montre quelques exemples pour des les orbitales des liaisons covalentes simples (liaisons sigma, de forme radiale, ici entre deux sous-couches s ou entre deux sous-couches p) ou doubles (liaison pi, non radiale, ici entre deux sous-couches p).

La table suivante montre toutes les orbitales atomiques jusqu'à 7s². Elles sont suffisantes pour caractériser tous les électrons à l’état fondamental d’un atome ou d’un ion simple, pour tous les éléments de la classification périodique, jusqu’au copernicium.

• Chaque image dans une même cellule montre la forme des orbitales pour chaque valeur possible du nombre quantique magnétique m (les deux orbitales de spins opposés sont de forme identique).
• En dessous le nombre N indique le numéro atomique minimum (impair) de l’élément dont au moins un électrons occupe une des orbitales correspondantes, et le numéro atomique maximum (pair) de l’élément dont les paires d’électrons occupent toutes les orbitales correspondantes.

	s1 à s2 (l = 0)	p1 à p6 (l = 1)	d1 à d10 (l = 2)	f1 à f14 (l = 3)
n = 1
n = 2
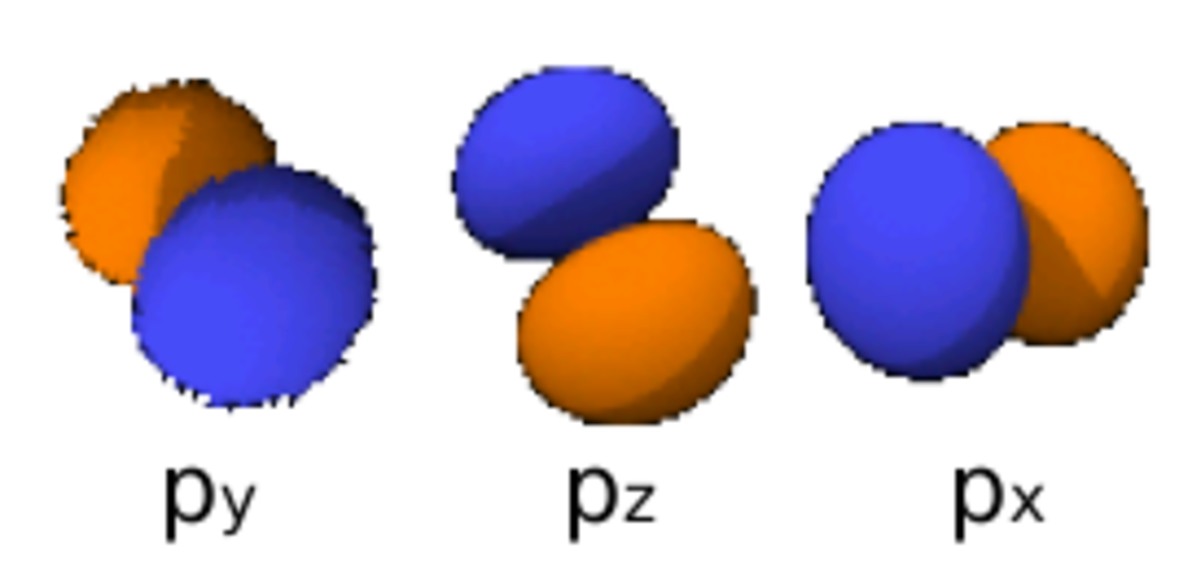
n = 3
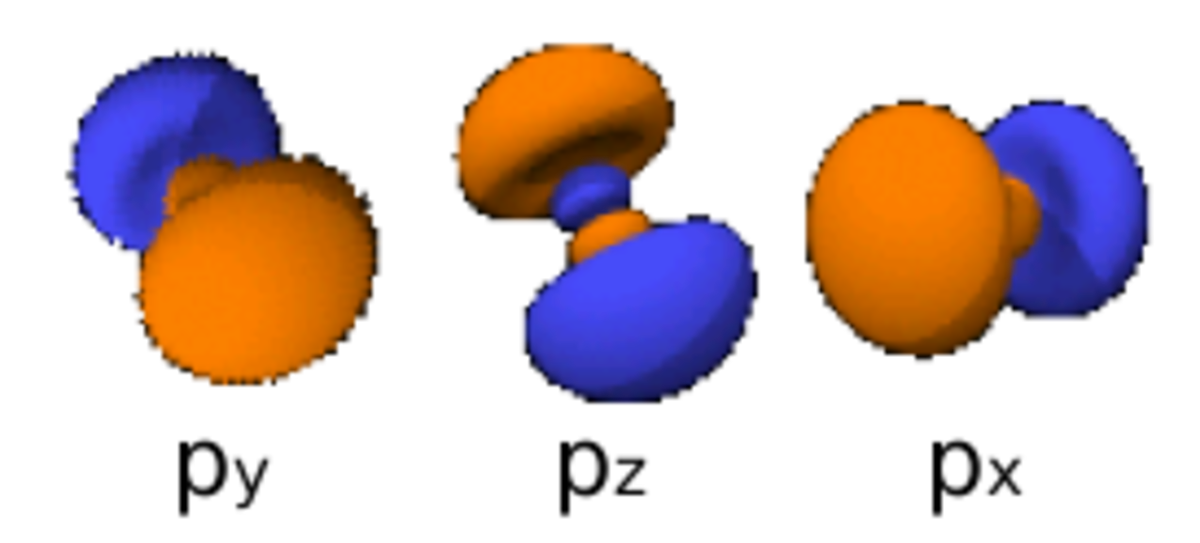
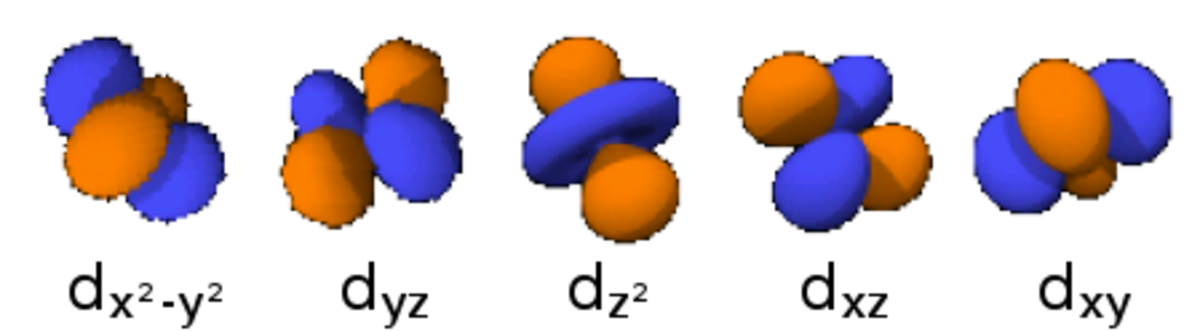
n = 4
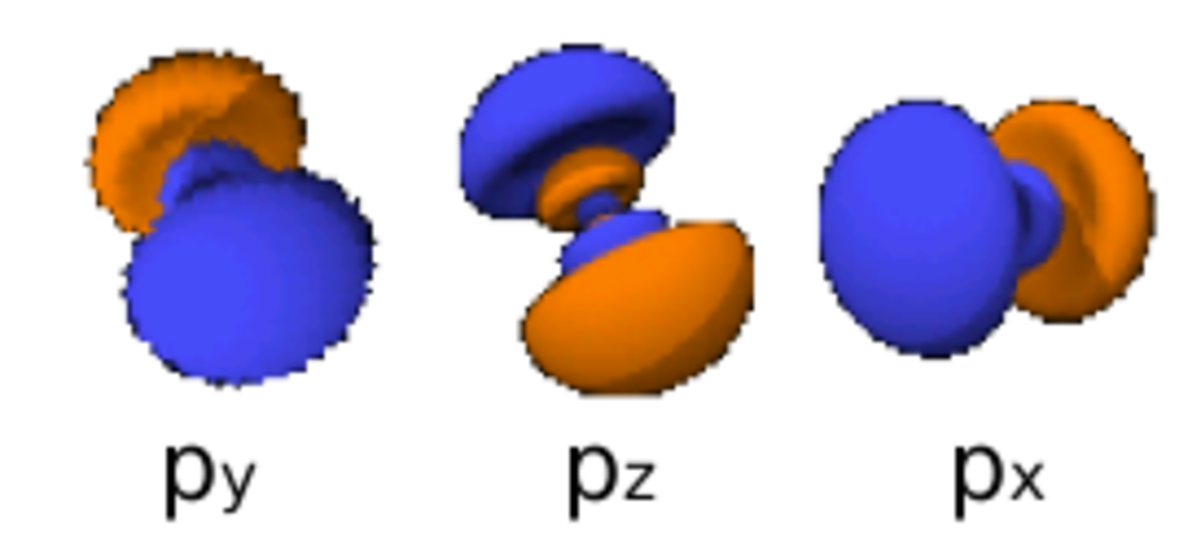
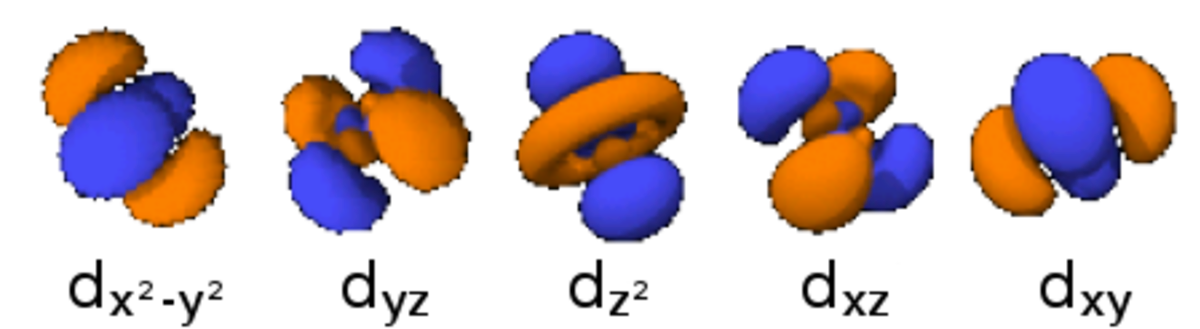
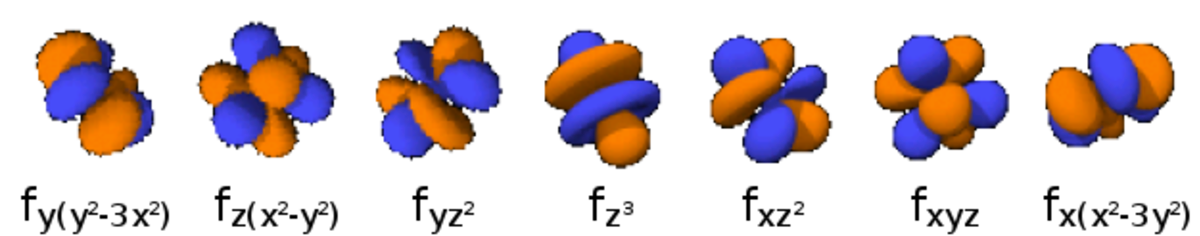
n = 5				. . .
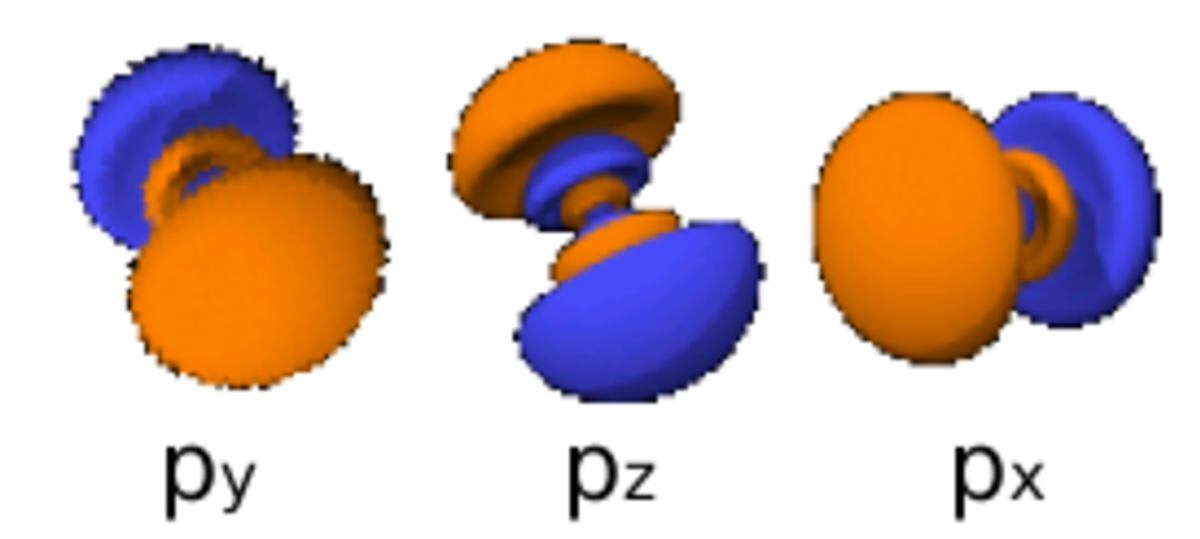
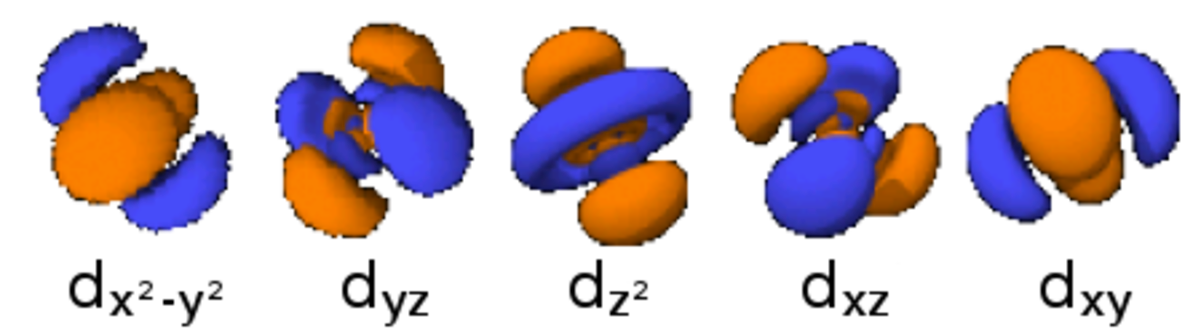
n = 6			. . .	. . .
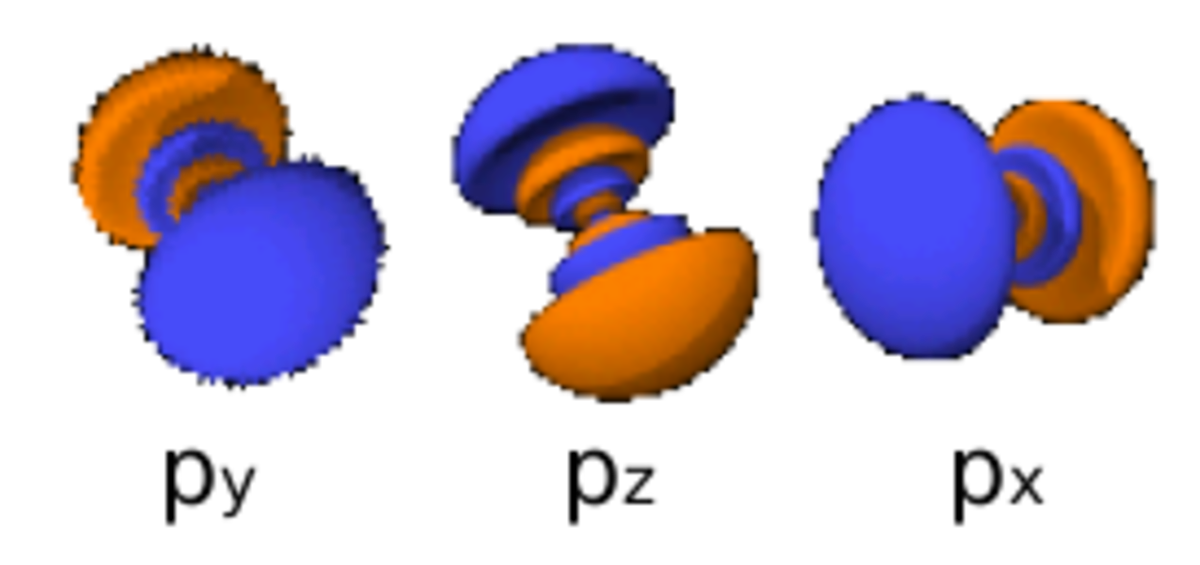
n = 7		. . .	. . .	. . .