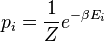Ensemble canonique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En physique statistique, l’ensemble canonique est un ensemble statistique, dans lequel chaque système est en équilibre avec un réservoir externe d'énergie. Cela signifie que le système peut échanger de l'énergie avec le réservoir, autrement dit, l’énergie est alors amenée à fluctuer d’un système à un autre de l'ensemble.
| Tableau résumant les ensembles en physique statistique | Ensembles | ||
| Microcanonique | Canonique | Grand-canonique | |
| Variables indépendantes | E, N, V ou B | T, N, V ou B | T, μ, V ou B |
| Fonction microscopique | Ω | ||
| Potentiel thermodynamique | |||
Principe
La détermination de la distribution des niveaux d'énergies au sein d'un ensemble canonique se fait en considérant l'ensemble microcanonique qu'il constitue avec le réservoir d'énergie. On établit alors la relation d'équilibre thermodynamique en recherchant la valeur maximale de l'entropie du système ainsi composé.
L'entropie étant une valeur extensive, l'entropie du système est la somme des entropies :
Stotale = Scanonique + Sreservoir
Les deux systèmes n'interragissent qu'en s'échangeant une énergie δE, de telle sorte que l'on peut écrire :

Cette valeur n'est nulle que lorsque l'on a :
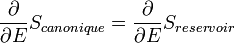
Ce qui suggère d'introduire le facteur :
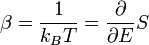
Le nombre de micro-états du système total peut s'écrire :
Ωtotal = ΩreservoirΩcanonique
On cherche à exprimer Ωcanonique, car la probabilité de trouver l'ensemble canonique à un certain niveau d'énergie lui est proportionnelle.
En passant aux logarithmes, on a :
lnΩcanonique = Stotal − Sreservoir = − ΔStotal = − βEcanonique
Car on peut considérer que l'énergie totale concédée à l'ensemble canonique est faible devant l'énergie totale du réservoir.
On a donc bien :
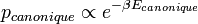
pour trouver le coefficient de proportionnalité, il suffit d'exprimer le fait que la somme de toutes ces probabilités est égale à 1. Pour cela on introduit donc la fonction de partition canonique :
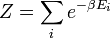
Et ainsi :