Entier quadratique - Définition

Outils et théorèmes

Conjugué et norme

Deux applications sont ont un rôle privilégié dans les corps quadratiques.

• L'application de Q[√d] dans lui-même qui à au nombre a + b.√d associe a - b.√d est dite application conjuguée.

L'article Extension quadratique montre qu'il n'existe que deux automorphismes de corps. Un automorphisme est un morphisme bijectif et un morphisme désigne une application respectant la structure, ici les deux opérations d'addition et de multiplication. Un morphisme φ vérifie :

Les deux automorphismes sont l'identité et l'application conjuguée. On remarque que si d est égal à -1, on retrouve le terme conjugué des nombres complexes.

La deuxième application importante est la suivante :

• L'application de Q[√d] dans Q qui à un nombre quadratique associe le produit de ce nombre par son conjugué est appelé norme.

Dans le reste de l'article, l'application norme est noté N. Dans le cas où d est égal à -1, on trouve le carré de la norme géométrique usuel. On peut se poser la question de savoir pourquoi les arithméticiens omettent d'ajouter la racine, à la différence des géomètres. La raison est la nature de l'ensemble d'arrivée de la fonction, il est égal à Q, ce qui n'est plus vrai avec la définition des géomètres. Cette propriété est essentielle pour de nombreux usages.

Si d est un entier positif, la norme n'a pas de raison d'être positive. La norme du nombre quadratique a + b.√d est a² - d.b². Si d est égal à 2, a à 1 et b à 1, on trouve en effet -1.

• L'application norme de Q[√d] respecte la multiplication :

Cette propriété est une conséquence directe de la définition de la norme, si α et β désignent deux nombres quadratiques de Q[√d], α' et β' leurs conjugués, alors :

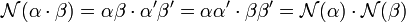
• L'application congugué est un automorphisme de l'anneau des entiers de Q[√d] et, sur cet ensemble, la norme est à valeur dans Z.

On remarque que si α est un entier quadratique, son conjugué possède le même polynôme minimal, il est donc aussi entier quadratique. L'application conjuguée est injective sur A car elle l'est sur K. Comme l'application est involutive, c'est-à-dire que le conjugué du conjugué est l'élément initial, elle est nécessairement surjective. Puisque l'application conjugué est un morphisme dans K, il l'est nécessairement dans un sous-ensemble et a fortiori dans la fermeture intégrale. Soit α' le conjugué de α. On a déjà démontré que le produit de deux entiers quadratiques est encore un entier quadratique, on en déduit que α.α' est un entier quadratique élément de Q, il est donc élément de Z, d'après la proposition précédente.

Si ω est égal à √d, la norme prend la forme (1), si d est congru à 1 modulo 4 et que ω est égal à 1/2(1 + √d) elle prend la forme (2) :

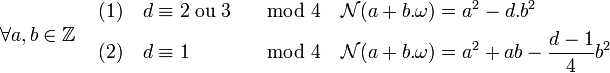
Groupe des unités

La première difficulté à résoudre pour comprendre la structure d'un anneau d'entiers quadratiques est son groupe des unités, c'est-à-dire le groupe formé par les éléments inversibles et munis de la multiplication. Une première remarque simplifie l'analyse, un entier quadratique est inversible si et seulement si sa norme est égale à ±1. Ce qui ramène la question à l'étude d'une des deux équations diophantienne x² - d.y² = ±1 ou si d est congru à 1 modulo 4 et si f désigne l'entier tel que d = 4f - 1 : x² + x.y - f.y² = ±1.

La première équation est étudiée depuis Diophante et porte le nom d'équation de Pell-Fermat. Elle est résolue de manière algorithmique par Bhaskara II un mathématicien indien du XII^e siècle et par Joseph Louis Lagrange en 1767 de manière théorique, à l'aide des fractions continues.

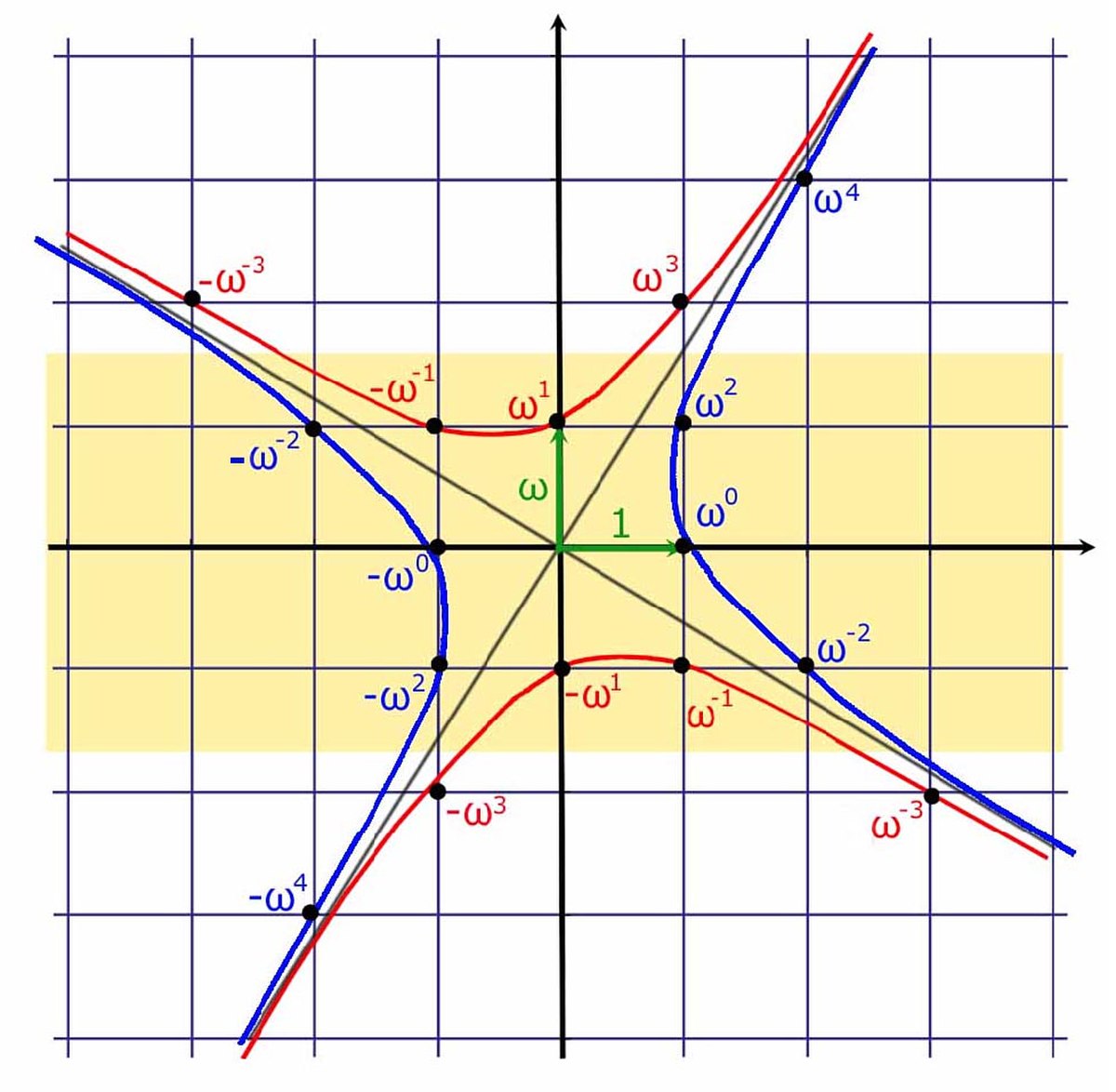
Si d est strictement négatif, le groupe est réduit à ±1, sauf dans les cas où d est égal à -1, le groupe contient alors 4 éléments (cf l'article Entier de Gauss), ou si d est égal à -3 et il en contient 6. Si d est strictement positif, le groupe des unités contient une infinité de solutions. Plus précisément, il est isomorphe à Z/2Z x Z. Il existe une unique unité ρ dont les deux coordonnées sont positives et tel que toutes les autres s'expriment sous la forme e.ρ ^k où e est égal à ±1 et k un élément de Z. Il existe deux algorithmes célèbres et relativement efficaces pour trouver cette unité dite fondamentale.

Graphiquement si l'on représente l'anneau à l'aide du repère orthonormal (1, ω) les points de l'anneau se situent sur le quadrillage régulier contenant le point 0 et formé de carrés de côté 1. Les éléments du groupe des unités se trouvent sur 4 branches d'hyperboles qui s'obtiennent par rotations successives d'un quart de tour.

L'analyse du groupe des unités ne nécessite pas l'usage des propriétés de fermeture intégrale de l'anneau. En conséquence, les résultats sont encore vrais pour un anneau d'entiers quadratiques quelconque.

Décomposition en idéaux premiers

La deuxième obstruction est la conséquence des idéaux premiers mais non principaux. On a vu qu'ils induisent des décompositions multiples d'un entier quadratique en facteurs premiers. Deux théorèmes permettent encore de travailler malgré cette obstruction, ils ne s'appliquent que sur des fermetures intégrales, c'est-à-dire que l'anneau doit contenir tous les entiers quadratiques.

La manière d'analyser cette situation pour Ernst Kummer est de considérer qu'il manque des nombres irréductibles. Les idéaux premiers sont alors vus comme les nombres premiers manquants. L'objectif consiste à ne plus décomposer un nombre mais un idéal :

• Tout idéal de l'anneau des entiers d'un corps quadratique Q[ω] se décompose de manière unique, à l'ordre près, en un produit d'idéaux premiers.

Pour étudier un tel anneau, il devient nécessaire d'expliciter les idéaux premiers. La majorité consiste en idéaux principaux et quelques autres ne le sont pas. Un deuxième théorème précise :

• Il n'existe qu'un nombre fini d'idéaux premiers non principaux dans l'anneau des entiers d'un corps quadratique.

Le théorème de Stark-Heegner précise pour quels entiers d l'anneau est principal si d est négatif :

• L'anneau des entiers du corps quadratique Q[√d] pour les valeurs de d réduites et négatives est principal si, et seulement si, d est une des valeurs suivantes : −1, −2, −3, −7, −11, −19, −43, −67 ou −163.

Dans le cas des entiers d positifs, les anneaux principaux sont beaucoup plus nombreux. En 2008, il est conjecturé qu'il en existe une infinité.