Entier quadratique - Définition
La liste des auteurs de cet article est disponible ici.
Applications
Classification des nombres premiers
La structure des entiers sur les corps quadratiques amène à étudier non pas les diviseurs d'un nombre premier p, mais les facteurs premiers de l'idéal pZ[u]. Cette analyse est utile pour la résolutions d'équations diophantiennes.
Nombre premier inerte
La première situation est celle où pZ[u] est un idéal premier :
-
- On dit que p est inerte dans Z[u] si l'idéal principal engendré par p est premier.
-
- Le nombre premier p est inerte si et seulement si -d n'est pas un résidu quadratique modulo p.
-
- Le corps premier Z[u]/pZ[u] est isomorphe à Fp2.
-
- Le nombre premier p est inerte si et seulement si -d n'est pas un résidu quadratique modulo p :
Le nombre premier p est inerte, si et seulement s'il n'existe pas de morphisme de Z[u] dans un le corps fini Fp à p élément. En effet, si un tel morphisme existe, son noyau est un idéal premier de norme p et si un idéal premier de norme p existe alors le morphisme de Z[u] dans le quotient remplit la condition.
Un tel morphisme existe si et seulement s'il est possible d'associer à √d une valeur dans Fp, la seule valeur possible est une racine de l'équation X2 = d, c'est-à-dire que d est résidu quadratique modulo p. Si tel est le cas, il existe une unique manière de prolonger l'application m qui à 1 associe 1 et à √d une de ces deux racines quadratiques dans Fp. Comme l'idéal pZ[u] est premier un tel morphisme n'existe pas un tel morphisme n'existe pas et -d n'est pas un résidu quadratique modulo p.
-
- Le corps premier Z[u]/pZ[u] est isomorphe à Fp2 :
La norme de pZ[u] est égal à p2. Si p est inerte, Z[u]/pZ[u] est un corps de cardinal la valeur absolue de norme de p, c'est-à-dire p2. Il n'existe qu'un unique corps contenant p2 éléments : Fp2, ce qui permet de conclure.
Nombre premier décomposé
La deuxième situation est celle où pZ[u] n'est pas premier et contient dans sa décomposition deux idéaux premiers :
-
- On dit que p est décomposé si son idéal principal contient deux idéaux premiers distincts.
Soit σ l'endomorphisme de Z[u] qui à 1 associe 1 et à √d associe -√d. Cette application est un morphisme d'anneau. L'application σ est dite conjugué. Dans le cas où d est négatif, elle se confond avec la fonction conjugué des nombres complexes.
-
- Les deux idéaux sont conjugués l'un de l'autre et ce sont les seuls idéaux de norme p.
L'anneau quotient Z[u] / pZ[u] est isomorphe au produit FpxFp.
-
- Les deux idéaux sont conjugués l'un de l'autre et ce sont les seuls idéaux de norme p.
Remarquons tout d'abord que la norme de p est égal à p2. Comme le produit des normes d'idéaux est égal à la norme du produit des idéaux et que le seul idéal de norme 1 est Z[u], la décomposition en idéal premier de pZ[u] ne peut contenir plus de deux idéaux distincts. Supposons qu'elle contienne exactement deux idéaux distincts M1 et M2.
Alors les normes de M1 et M2 sont égales à p et Z[u]/Mi, si i est égal à 1 ou à 2, est isomorphe au corps premier de cardinal p. Le paragraphe précédent montre qu'il existe un élément r du corps premier Fp tel que r2 est égal à -d. Il existe exactement deux morphismes de corps de Z[u] dans Fp, ils associent à 1 la valeur 1 dans Fp et à √d respectivement les valeurs r et -r. Les idéaux M1 et M2 sont les deux noyaux respectifs de ces deux morphismes. Ces deux morphismes sont conjugués, leurs noyaux le sont donc aussi.
-
- L'anneau quotient Z[u] / pZ[u] est isomorphe au produit FpxFp :
Montrons que l'intersection de M1 et M2 est égal au produit M1.M2. Remarquons que le produit est nécessairement inclus dans l'intersection. Réciproquement soit m un élément de l'intersection. Comme ces deux idéaux sont maximaux et distincts, M1 + M2 est égal à Z[u], et 1 est la somme d'un élément de M1 et d'un élément de M2 : m1 + m2 = 1 et donc m.m1 + m.m2 = m, ce qui démontre l'égalité.
Le théorème chinois généralisé et le fait que Z[u] / Mi soit le corps à p éléments montrent que :
![\frac {\mathbb Z[u]}{p\mathbb Z[u]}=\frac {\mathbb Z[u]}{\mathfrak M_1 \cdot \mathfrak M_2}= \frac {\mathbb Z[u]}{\mathfrak M_1 \cap \mathfrak M_2}= \frac {\mathbb Z[u]}{\mathfrak M_1}\times \frac {\mathbb Z[u]}{\mathfrak M_2}=\mathbb F_p\times\mathbb F_p](https://static.techno-science.net/illustration/Definitions/autres/7/7d82af0889d44f854792e6a59c016dac_88e5c87413c8832bca89957f5ee5e3d7.png)
Nombre premier ramifié
Il se peut que pZ[u] ne soit contenu que dans un unique idéal premier :
-
- On dit que p est ramifié s'il existe un unique idéal premier M contenant p et que pZ[u] n'est pas premier.
Si ce cas se produit, alors
-
- Si le nombre premier p est ramifié, l'idéal pZ[u] est égal au carré de l'unique idéal premier contenant p.
-
- Le nombre premier p est ramifié, si et seulement s'il divise le discriminant de l'anneau Z[u].
L'anneau quotient Z[u] / pZ[u] est de cardinal p2 et contient au moins un élément nilpotent, non nul.
-
- Si le nombre premier p est ramifié, l'idéal pZ[u] est égal au carré de l'unique idéal M premier contenant p :
Il a déjà été démontré que la décomposition de pZ[u] est le produit d'un ou deux idéaux premiers. Si p n'est pas premier, alors pZ[u] est un produit de deux idéaux premiers. Comme il n'en existe qu'un, noté M, contenant l'idéal pZ[u], il est nécessairement égal à M2.
-
- L'anneau quotient Z[u] / pZ[u] contient au moins un élément nilpotent :
M contient un élément qui n'est pas multiple de p car, par hypothèse M n'est pas égal à l'idéal engendré par p. Soit α la classe de cet élément dans Z[u] / pZ[u]. Comme le carré de M est égal à pZ[u], α2 est nul. L'élément α n'est pas nul dans Z[u] / pZ[u] car il contient un représentant qui n'est pas dans M, en revanche son carré l'est. Ce qui montre que l'anneau quotient contient au moins un élément nilpotent.
-
- Le nombre premier p est ramifié, si et seulement s'il divise le discriminant de l'anneau Z[u].
Supposons que p soit ramifié, le quotient de Z[u] par pZ[u] est un Fp espace vectoriel. Il contient un élément non nul α nilpotent d'ordre deux. L'élément α n'est pas colinéaire à la classe de 1 car aucun multiple de 1 n'est nilpotent, (1, α) forme donc une base de l'espace vectoriel quotient. Soit x et y deux vecteurs de coordonnées (x1, x2) et (y1, y2) dans la base (1, α). La matrice Μxy de l'homothétie de rapport xy est la suivante :
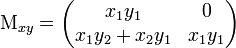
On en déduit la forme trace et la matrice T associée :
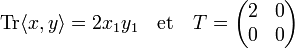
Le déterminant de T est ainsi nul. Ce déterminant est le quotient dans Z/pZ du discriminant de l'anneau Z[u]. On en déduit que le discriminant est un multiple de p, ce qu'il fallait démontrer.
Réciproquement, si p n'est pas un diviseur du discriminant, le déterminant de T dans le quotient Z[u] / pZ[u] est, à un facteur multiplicatif près, la classe du discriminant de Z[u] dans Z/pZ qui n'est pas nul. En conséquence, il n'existe pas d'élément nilpotent, ce qui montre que p ne peut être ramifié.
Equation diophantienne
La raison initiale du développement des corps quadratiques est l'étude d'équations diophantiennes d'ordre deux. Illustrons par deux exemples comment la théorie précédente permet de venir à bout de questions de cette nature.
x2 + 2.y2 = p
Le cas d égal à -1 ou à -3 est traité dans l'article théorème des deux carrés de Fermat. Ici, d est égal à -2 :
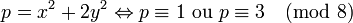
En effet, calcul analogue à celui présenté pour les entiers de Gauss montre que l'anneau est euclidien donc principal. S'il existe un idéal contenant p éléments, comme il est principal et que sa norme est égale à p, le tour est joué. Cette méthode s'applique à tous les anneaux d'entiers euclidiens.
Dans un premier temps déterminons les valeurs de p tel que -2 est un résidu quadratique. L'article Loi de réciprocité quadratique montre que -1 est un carré si et seulement si p est congru à 1 modulo 4. La valeur 2 est un carré si et seulement si p est congru à 1 ou à 7 modulo 8. On obtient le tableau suivant :
|
Le signe + signifie que la valeur est un carré pour un nombre premier congru à la valeur de la première ligne modulo 8. On en conclut que -2 est un carré modulo p si et seulement si p est congru à 1 ou à 3.
Si cette condition n'est pas remplie, il est impossible de construire un morphisme de Z[i√2] dans Z/pZ, ce qui montre que p est inerte et qu'il n'y a pas de solution.
Si p est congru à 1 ou à 3 modulo 8, il existe dans Z/pZ une valeur r de carré égal à -2. L'application qui à l'entier algébrique a + b.i√2 associe a + b.r dans Z/pZ est un morphisme d'anneau. Son noyau est un idéal de Z[i√2]. Comme l'anneau est euclidien, l'idéal est principal, soit α + β.i√2 un générateur. La norme de ce générateur est égal au cardinal de l'anneau quotient, en l'occurrence p. La norme de l'idéal est aussi la valeur absolue de la norme d'un générateur. Elle est égale à α2 + 2.β2 et à p. Ce qui résout l'équation.
x2 + 5.y2 = p
Si d est égal à 5, la situation est plus délicate car l'anneau Z[i√5] n'est pas euclidien, elle se résume de la manière suivante :
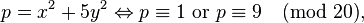
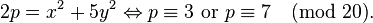
Si initialement la méthode est la même que pour le cas euclidien, il devient nécessaire d'établir la nature des idéaux de norme p. S'il est principal, une solution existe, sinon la valeur p n'est pas atteinte par la fonction. Le groupe des classes permet de s'en rendre compte. Cette méthode est générale, cependant pour des valeurs importantes de d les calculs s'avèrent fastidieux.
Dans un premier temps recherchons les nombres premiers inertes. L'application de la loi de réciprocité quadratique montre que 5 est un résidu quadratique modulo p si et seulement si p est un résidu quadratique modulo 5. Or Z/5Z contient deux classes de résidus, celle de 1 et celle de 4. On en déduit le tableau suivant, construit comme précédemment :
|
Un raisonnement analogue au précédent montre que les classes de 11, 13, 17 et 19 sont inertes.
Il reste quatre classes ramifiées ou décomposées. Il s'agit de déterminer si les idéaux associés sont principaux ou non. Pour cela examinons le groupe des classes de l'anneau. Un résultat établi précédemment montre que toute classe contient un idéal de norme inférieure à 4.√5 / π. Comme la norme est un entier relatif, la seule valeur possible pour un représentant d'une classe différente de celle des idéaux principaux est 2. On vérifie qu'un unique idéal : M2 contenant 2 et 1 + i.√5 est de norme 2. Il n'est pas principal car aucun élément de l'anneau n'a pour norme en valeur absolue 2.
-
- Le groupe des classes de l'anneau d'entiers algébriques Z[i√5] est d'ordre 2.
Le discriminant de Z[i√5] est égal à -20, l'idéal M2 est ramifié et l'anneau quotient Z[i√5] / M2 contient des éléments nilpotents comme 1 + i.√5, dont le carré est multiple de 2.
L'existence d'un idéal premier non principal de norme 2 amène à étudier la parité des solutions de l'équation. Soit a et b deux entiers relatifs premiers entre eux tel que a2 + 5.b2 soit un multiple de p. Si la somme est paire, les entiers a et b sont impairs et donc congru à 1 ou à 3 modulo 4. Leur carré est congru à 1 modulo 8, en conséquence a2 + 5.b2 est congru à 6 modulo 8 et p est congru à 3 modulo 4. Dans ce cas là, p est congru à 3 ou 7 modulo 20. Si la somme est impaire, l'un des deux nombres est pair et l'autre impair, le carré de celui impair est congru à 1 modulo 4 et l'autre est un multiple de quatre. La somme est donc congru à 1 modulo 4 et p est congru à 1 ou 9 modulo 20.
Si p est congru à 3 ou à 7 modulo 20, l'équation ne peut admettre de solution égale à p car toute solution est paire. En conséquence, aucun idéal Mp de norme p ne peut être principal, il serait en effet généré par une solution de l'équation. En revanche, l'idéal M2.Mp l'est car le groupe des classes est d'ordre deux et M2 n'est pas principal. L'idéal M2.Mp est de norme 2.p, il contient un générateur et sa norme est égal à 2.p, ce qui revient à dire que si p est congru à 3 ou 7 modulo 20, l'équation x2 + 5.y2 = 2.p admet une solution.
Si p est congru à 1 ou à 9 modulo 20, l'équation x2 + 5.y2 = 2p ne peut admettre de solution. Le raisonnement précédent montre que M2.Mp ne peut être principal et donc Mp l'est, ce qui permet de conclure.

















































