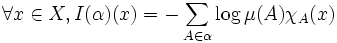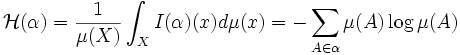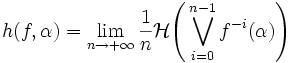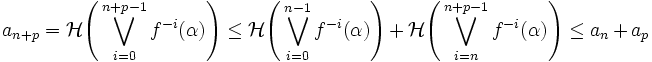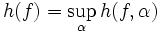Entropie métrique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et plus précisément, dans la théorie des systèmes dynamiques, l'entropie métrique, ou entropie de Kolmogorov (appelée également en anglais measure-theoretic entropy) est un outil développé par Kolmogorov vers le milieu des années 1950, issu du concept probabiliste d'entropie de la théorie de l'information de Shannon. Kolmogorov montra comment l'entropie métrique peut être utilisée pour montrer si deux systèmes dynamiques ne sont pas conjugués. C'est un invariant fondamental des systèmes dynamiques mesurés. En outre, l'entropie métrique permet une définition qualitative du chaos : une transformation chaotique peut être vue comme une transformation d'entropie non nulle.
Construction de l'entropie métrique
Présentons tout d'abord le cadre mathématique dans lequel on se place.
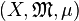
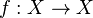
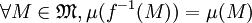
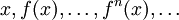
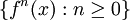
Si l'on se donne une partition finie α de X constituée d'ensembles mesurables
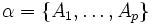
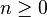
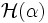
Entropie d'une partition
Soit α une partition finie de X en ensembles mesurables. Un point
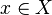
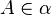
![I(\alpha) : X \to [0 ; + \infty ]](https://static.techno-science.net/illustration/Definitions/autres/d/dc4e8fa0d3a00b42a75e0e6e0f6dafd7_9535f3c6815edc20742cff9e2eaabb76.png)
c'est-à-dire I(α)(x) = − logμ(A) si
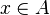
L'entropie de la partition α est la moyenne de I(α) :
On prend 0log0 égal à 0. Si α et β sont deux partitions mesurables de X, on définit le joint de α et β,
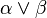
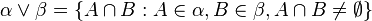
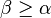
L'entropie d'une partition vérifie les propriétés intuitives suivantes :
- Si α et β sont deux partitions mesurables, alors
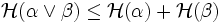
- Notons
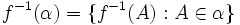
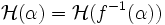
La première propriété signifie que l'information apportée par la connaissance simultanée des positions des états du système relativement à deux partitions est inférieure à la somme des informations apportées relativement à chacune des partitions. La deuxième propriété provient du fait que f préserve la mesure.
Entropie d'une transformation relativement à une partition
α est une partition mesurable. On définit l'entropie h(f,α) de la transformation f relativement à α par :
On peut voir la transformation f comme le passage d'un jour au suivant lors d'une expérience. Au temps zéro, on ne parvient pas à distinguer tous les états, on regroupe les états non distinguables par paquets, on forme de cette manière une partition α.
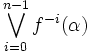
La limite définie existe bien. Si on note
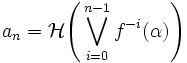
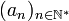
On a utilisé respectivement les deux propriétés de la section précédente.
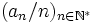
Dernière étape : entropie métrique d'une transformation
L'entropie métrique de f, notée h(f) est la borne supérieure des entropies de f relativement aux partitions finies mesurables de X
h(f) est éventuellement infinie.