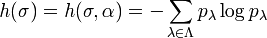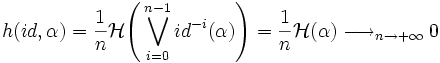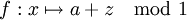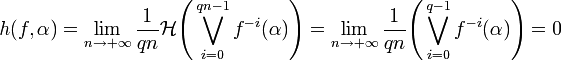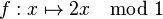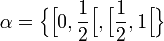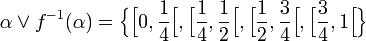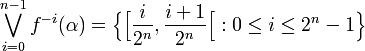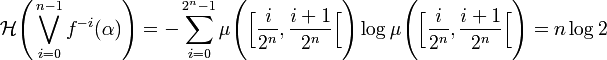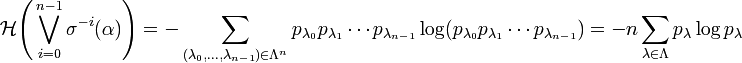Entropie métrique - Définition

Exemples de systèmes dynamiques et calcul d'entropie

Le calcul de l'entropie métrique est facilité lorsque la borne supérieure est atteinte, i.e lorsqu'il existe une partition α telle que l'entropie métrique et l'entropie relativement à α soient confondues. À titre d'exemple, traitons le cas de l'application identité de X. Alors,

L'identité a une entropie nulle, ce qui est prévisible en raison de son caractère peu chaotique.

Dans beaucoup de cas moins triviaux, le théorème suivant, de Kolmogorov-Sinai, est l'un des outils les plus pratiques pour calculer une entropie, car il évite de prendre la borne supérieure sur toutes les partitions mesurables de X.

Si α est une partition mesurable de X telle que la suite engendre la tribu , ou bien si f est inversible (f^-1 est mesurable et préserve la mesure) et la suite engendre la tribu alors on dit que α est génératrice.

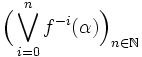
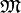
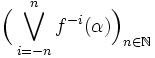
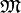
Le théorème de Kolmogorov-Sinai affirme que si α est génératrice, alors h(f) = h(f,α).

Rotations du cercle

est le cercle unité, muni de la mesure d'angle dθ. Analysons l'effet d'une rotation

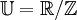
lorsque a = p / q est rationnel. Soit α une partition :

Dans le cas où a est irrationnel, on montre également que l'entropie métrique de f est nulle.

Doublement des angles

Toujours sur le cercle unité, on prend cette fois l'application

qui double les angles. On considère la même partition

On observe que :

Puis par récurrence, on déduit plus généralement que :

Comme les ensembles du type engendrent la tribu , le théorème de Kolmogorov-Sinai montre que h(f) = h(f,α) et :

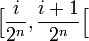
L'entropie métrique de f est donc log 2.

Décalage de Bernoulli

On dispose d'un alphabet fini . Soit des nombres strictement positifs de somme 1. On assigne à chaque lettre i la probabilité m({i}) = p_i d'apparition. (Λ,2^Λ,m) est un espace de probabilité. On introduit l'espace des mots infinis . On définit l'application décalage σ par σ(x)_n = x_{n + 1} pour . est un système dynamique inversible. On partitionne en où P_i est l'ensemble des mots tels que x₀ = i. est la partition par les cylindres . L'ensemble de ces cylindres engendrent la tribu de et le théorème de Kolmogorov-Sinai s'applique. On calcule alors facilement :

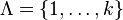
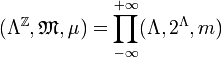
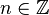
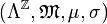
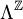
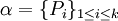
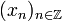
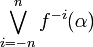
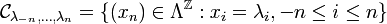
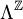
Donc .