Équation de Klein-Gordon - Définition
La liste des auteurs de cet article est disponible ici.
De l'équation de Klein-Gordon à l'équation de Dirac
Le fait que la densité ρ ne soit pas positive partout provient du fait que cette densité contient une dérivée première par rapport au temps, comme l'a remarqué Dirac en 1928. Ceci est lié au fait que l'équation de Klein-Gordon contient une dérivée temporelle seconde.
Approche naïve
Pour obtenir une équation relativiste du premier ordre en temps, on peut songer à quantifier directement l'expression :
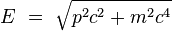
La procédure de quantification canonique conduit alors à l'équation :
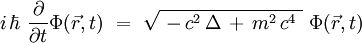
En raison de la présence d'une racine carrée sur l'opérateur aux dérivées partielles spatiales, cette équation semble a priori bien peu commode à résoudre. On sait aujourd'hui donner un sens mathématiquement précis à l'opérateur
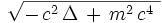
L'équation de Dirac
Dirac recherchera alors une autre équation relativiste du premier ordre en temps et en espace. Il commencera par essayer d'établir une relation de dispersion du type :
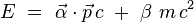
entre l'énergie, la masse et l'impulsion. Il réussira et, après quantification canonique, obtiendra au final une équation qui porte aujourd'hui son nom, l'équation de Dirac, et qui décrit très bien les fermions de spin un-demi comme l'électron. Le cadre pertinent pour interpréter cette équation quantique relativiste sans difficultés est encore celui de la théorie quantique des champs.

















































