Équation de Klein-Gordon - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'équation de Klein-Gordon (1926), parfois également appelée équation de Klein-Gordon-Fock, est une version relativiste de l'équation de Schrödinger décrivant des particules massives de spin nul, sans ou avec charge électrique.
L'équation de Klein-Gordon
Dérivation
L 'équation relativiste donnant l'énergie d'une particule massive isolée s'écrit :
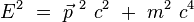
En appliquant les règles de quantification canonique issues de la mécanique quantique non relativiste, on obtient l'équation dite de Klein-Gordon :
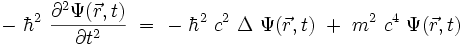
Cette équation se réécrit sous la forme suivante :
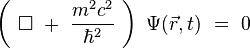
où

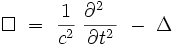
On peut également utiliser le formalisme relativiste (en unités naturelles) :
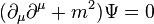
avec la convention :
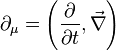
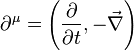
Difficultés d'interprétation
Les solutions de l'équation de Klein-Gordon présentent de sérieuses difficultés d'interprétation dans le cadre de la mécanique quantique originelle, théorie censée décrire une seule particule. Si l'on cherche par exemple à construire une densité de probabilité de présence qui vérifie l'équation relativiste de continuité :
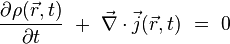
on obtient inévitablement les grandeurs suivantes :
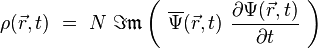
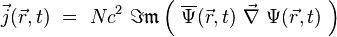
où
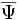
Le cadre pertinent pour interpréter cette équation quantique relativiste sans difficultés est la théorie quantique des champs
Aspects historiques
La querelle des origines
Bien qu'en 1925 Louis de Broglie ait trouvé une équation proche (avec un signe moins au second membre), cette contribution ne semble pas avoir retenu l'attention des physiciens.
Il est amusant de remarquer que, selon Dirac, Schrödinger aurait d'abord écrit l'équation relativiste dite aujourd'hui de Klein-Gordon, ceci pour tenter de décrire l'électron au sein de l'atome d'hydrogène. En effet, la lecture du premier mémoire de Schrödinger publié en février 1926 montre que celui-ci a déjà essayé une équation d'onde relativiste, mais ce premier mémoire ne contient pas l'équation écrite explicitement. Les prédictions obtenues n'étant pas conforme aux résultats expérimentaux assez précis obtenus par Paschen dès 1916, Schrödinger se serait alors aperçu que c'était l'équation non relativiste - dite aujourd'hui de Schrödinger - qui donnait le bon spectre pour l'hydrogène (après inclusion des effets de spin de façon ad hoc). Schrödinger n'a publié son équation relativiste que dans le quatrième mémoire de 1926.
Entre temps, plus précisément entre les mois d'avril et septembre 1926, pas moins de cinq autres articles, publiés indépendamment, contenaient l'équation dite aujourd'hui de Klein-Gordon. Les auteurs de ces cinq articles, dont les références figurent dans la bibliographie, sont : Klein, Gordon, Fock, de Donder et van den Dungen, et enfin Kudar.
Enfin, dans son second article de 1926, Fock introduit également la procédure de couplage minimal, décrivant le couplage de la particule massive de charge électrique e à un champ électromagnétique externe donné, représenté par un quadri-potentiel Aμ. Pour plus de détails, voir le paragraphe technique suivant.
Détails techniques
Couplage minimal
Pour une charge e en présence d'un champ électromagnétique externe donné, représenté par le quadri-potentiel Aμ, la prescription de couplage minimal de Fock conduit à substituer à la quadri-impulsion pμ la quantité suivante :
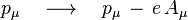
Introduisons explicitement les composante temporelle et spatiales de la quadri-impulsion :
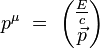
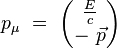
et du quadri-potentiel :
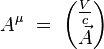
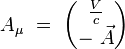
On obtient alors explicitement :
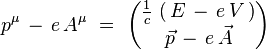
Dérivation de l'équation
On repart de l'équation de dispersion relativiste d'une particule massive isolée :
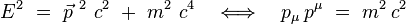
On y introduit le couplage minimal de Fock :
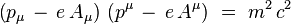
ce qui donne explicitement en substituant les composantes :
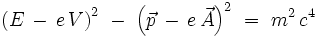
En présence d'un potentiel Coulombien statique décrivant l'interaction de l'électron avec un proton (supposé infiniment lourd), le potentiel vecteur est nul :
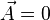
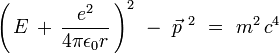
On applique la quantification canonique à cette équation classique, qui devient un opérateur aux dérivées partielles :
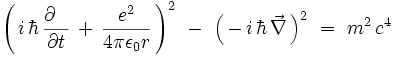
d'où l'équation dépendante du temps :
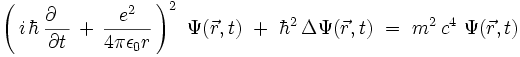
On recherche enfin les états stationnaires d'énergie Econstante sous la forme d'une fonction purement spatiale multipliée par une exponentielle oscillante en temps :
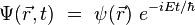
On obtient alors l'équation aux valeurs propres :
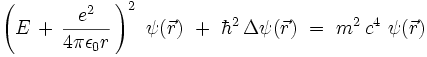
Schrödinger fût découragé par le fait que cette équation ne donne pas le spectre correct de l'atome d'hydrogène. On obtient en effet les niveaux d'énergie suivants :
![E_{n,l} \ = \ mc^2 \ \left[ \, 1 \, - \, \frac{\alpha^2}{2 \, n^2} \, - \, \frac{\alpha^4}{2 \, n^4} \ \left( \frac{n}{l + \frac12} \, - \, \frac{3}{4} \right) \, \right] \ + \ O(\alpha^6)](https://static.techno-science.net/illustration/Definitions/autres/6/648b218e05e41a11ec8bff42b3a5fb60_1708d6e79a2ceb17342a3ad33c39eb4b.png)
où le nombre quantique principal n est un nombre entier strictement positif, le nombre quantique orbital l est un nombre entier positif compris entre 0 et n − 1, et α est la constante de structure fine :
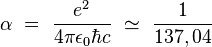
Le terme d'ordre α2 est correct, mais le terme suivant d'ordre α4, qui décrit la structure fine, n'est pas conforme aux résultats expérimentaux obtenus par Paschen dès 1916. L'expression correcte à cet ordre est en effet :
![E_{n,l} \ = \ mc^2 \ \left[ \, 1 \, - \, \frac{\alpha^2}{2 \, n^2} \, - \, \frac{\alpha^4}{2 \, n^4} \ \left( \frac{n}{j + \frac12} \, - \, \frac{3}{4} \right) \, \right] \ + \ O(\alpha^6)](https://static.techno-science.net/illustration/Definitions/autres/6/6ecb36ac6afdacc2e20137ec6230d6e5_9da8ff05576fd30d5e1c6b2033b6c2dc.png)
où le nombre quantique j = l + 1 / 2, le demi supplémentaire étant lié au spin de l'électron, qui n'est pas inclus dans l'équation de Klein-Gordon.

















































