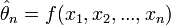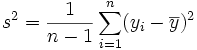Estimateur (statistique) - Définition
La liste des auteurs de cet article est disponible ici.
Définition formelle
Un estimateur du paramètre inconnu θ d'un modèle ou loi de probabilité est une fonction qui fait correspondre à une suite d'observations issues du modèle ou loi de probabilité la valeur
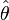
Construction d'estimateurs
Méthode du maximum de vraisemblance
Comme son nom l'indique, cette méthode consiste à maximiser une fonction appelée fonction de vraisemblance, contenant le paramètre que l'on souhaite estimer. Elle aura ainsi de fortes chances d'être très proche de ce paramètre.
Fonction de vraisemblance, au vu d'un n-échantillon (x1,...,xi,...,xn) :

L'estimateur obtenu par cette méthode est généralement le meilleur possible, mais cela peut être fastidieux et surtout nécessite de maîtriser des règles mathématiques plus difficiles que la méthode des moments (voir ci-dessous).
Méthode des moments
La méthode des moments permet d'estimer des paramètres : pour cela, on pose l'égalité entre moments théoriques et empiriques correspondants puis, en résolvant les équations écrites, on exprime les paramètres en fonction de ces moments.
Estimateurs classiques
On se placera dans le cas simple d'un tirage aléatoire de n individus dans une population en comportant N. On s'intéresse au caractère quantitatif Y de moyenne
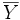
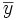
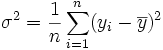
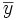
Estimateur de la moyenne de Y
On prend en général comme estimateur de
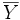
-
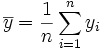
appelée moyenne empirique de Y. On démontre que c'est un estimateur sans biais, c’est-à-dire que
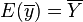
Estimateur de la variance de Y
On pourrait penser que σ2 est un bon estimateur de V(Y). Cependant des calculs (voir écart type) prouvent que cet estimateur est biaisé, l'espérance de σ2 est toujours inférieure à V(Y). On prouve qu'un estimateur sans biais de V(Y) est :
-
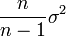
-
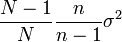
On peut remarquer que, pour N grand, le calcul avec remise et le calcul sans remise donnent des résultats presque équivalents. (le quotient
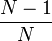
appelée variance empirique de Y.
Efficacité, convergence et intervalle de confiance
La manière dont
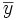
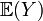
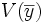
-
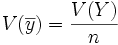
-
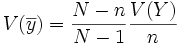
On peut remarquer que, pour N très grand devant n, les deux valeurs sont très voisines. Par la suite, on ne s'intéressera donc qu'au cas du tirage avec remise en considérant que N est très grand.
On s'aperçoit que plus n est grand, plus
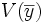
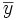
L'inégalité de Bienaymé-Tchebychev précise que, pour tout réel strictement positif ε,
donc que
Or
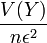
 : l'estimateur
: l'estimateur
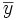
Enfin, il résulte du théorème de la limite centrale que pour n relativement grand, la variable aléatoire
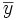
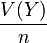
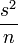
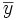
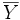
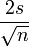
![\left[\overline Y - \frac{2\sigma(Y)}{\sqrt n}, \overline Y +\frac{2\sigma(Y)}{\sqrt n}\right]](https://static.techno-science.net/illustration/Definitions/autres/a/abda8357d48b0497cd2f2dee0354b2ce_435537d109050fc005a1f6e3ff477a75.png)
On parle souvent de la précision d'une enquête : c'est le rapport
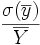
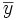
![[0,96 \overline Y, 1,04 \overline Y]](https://static.techno-science.net/illustration/Definitions/autres/d/d9d22c603d9c4fdd05ba2beadeaa8084_3524ffd1f34004e27cecbd0ac5ce2ee4.png)
Influence des techniques de sondages sur les estimateurs
Découper la population en strates homogènes peut réduire de manière significative la valeur de la variance de l'estimateur et donc le rendre plus efficace.
Utiliser un tirage aléatoire à probabilités inégales, procéder à un sondage en plusieurs étapes ou par grappe change évidemment les formules calculées précédemment.
Enfin, l'utilisation d'informations auxilaires permet parfois d'effectuer une correction sur l'estimateur pour le rapprocher de la valeur réelle.