Estimateur (statistique) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En statistique inférentielle, un estimateur est une valeur calculée sur un échantillon et que l'on espère être une bonne évaluation de la valeur que l'on aurait calculée sur la population totale. On cherche à ce qu'un estimateur soit sans biais, convergent, efficace et robuste.
Exemple d'estimateurs
Si l'on cherche à évaluer la taille moyenne des enfants de 10 ans, on peut effectuer un sondage sur un échantillon de la population des enfants de 10 ans (par exemple en s'adressant à des écoles réparties dans plusieurs milieux différents). La taille moyenne calculée sur cet échantillon, appelée moyenne empirique, sera un estimateur de la taille moyenne des enfants de 10 ans.
Si l'on cherche à évaluer la surface totale occupée par la jachère dans un pays donné, on peut effectuer un sondage sur plusieurs portions du territoire de même taille, calculer la surface moyenne occupée par la jachère et appliquer une règle de proportionnalité.
Si l'on cherche à déterminer le pourcentage d'électeurs décidés à voter pour le candidat A, on peut effectuer un sondage sur un échantillon représentatif. Le pourcentage de votes favorables à A dans l'échantillon est un estimateur du pourcentage d'électeurs décidés à voter pour A dans la population totale.
Si l'on cherche à évaluer la population totale de poissons dans un lac, on peut commencer par ramasser n poissons, les baguer pour pouvoir les identifier ultérieurement, les relâcher, les laisser se mélanger aux autres poissons. On tire alors un échantillon de poissons du lac, on calcule la proportion p de poissons bagués. La valeur n/p est un estimateur de la population totale de poissons dans le lac. S'il n'y a aucun poisson bagué dans l'échantillon, on procède à un autre tirage.
Un estimateur est très souvent une moyenne, une population totale, une proportion ou une variance.
Qualité d'un estimateur
Un estimateur est une valeur
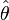
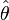
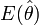
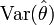
Biais
Une variable aléatoire fluctue autour de son espérance. On souhaite donc que l'espérance de
![\operatorname{Biais}(\hat\theta)\equiv E[\hat\theta]-\theta](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/77c4c1655115d2f0ad5662cf3c3dfd2f_0bda1ae5aa996e6036e4b3e89d10bd3d.png)
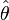
Lorsque l'espérance de l'estimateur
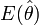
L'estimateur choisi précédemment sur la taille moyenne des enfants de 10 ans est un estimateur sans biais mais celui des poissons comporte un biais: le nombre de poissons estimé est en moyenne supérieur au nombre de poissons réels.
Erreur quadratique moyenne
L'erreur quadratique moyenne est l'espérance du carré de l'erreur entre la vraie valeur et sa valeur estimée.
Définition —
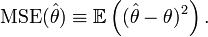
Convergence
On souhaite aussi pouvoir, en augmentant la taille de l'échantillon, diminuer l'erreur commise en prenant
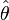
Définition — L'estimateur
.
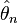
On l'interprète comme le fait que la probabilité de s'éloigner de la valeur à estimer de plus de ε tend vers 0 quand la taille de l'échantillon augmente.
Cette définition est parfois écrite de manière inverse:
Définition — L'estimateur
.
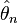
Il existe enfin un type de convergence plus forte, la convergence presque sûre, définie ainsi pour un estimateur:
Définition — L'estimateur
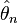
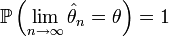
Exemple: La moyenne empirique est un estimateur convergent de l'espérance d'une variable aléatoire. La loi des grands nombres dans sa version "faible" assure que la moyenne converge en probabilité vers l'espérance et la loi forte des grands nombres qu'elle converge presque sûrement.
Taux de convergence
Efficience
La variable aléatoire fluctue autour de son espérance. Plus la variance
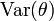
Robustesse
Il arrive que lors d'un sondage, une valeur extrême et rare apparaisse (par exemple un enfant de 10 ans mesurant 1,80 m). On cherche à ce que ce genre de valeur ne change que de manière très faible la valeur de l'estimateur. On dit alors que l'estimateur est robuste.
Exemple: En reprenant l'exemple de l'enfant, la moyenne n'est pas un estimateur robuste car ajouter l'enfant très grand modifiera beaucoup la valeur de l'estimateur. La médiane par contre n'est pas modifiée dans un tel cas.
