Système de coordonnées - Définition

Introduction

En mathématiques, un système de coordonnées permet de faire correspondre à chaque point d'un espace à N dimensions, un N-uplet de scalaires. Dans beaucoup de cas, les scalaires considérés sont des nombres réels, mais il est possible d'utiliser des nombres complexes ou des éléments d'un corps quelconque. Plus généralement, les coordonnées peuvent provenir d'un anneau ou d'une autre structure algébrique apparentée.

On considère que l'espace existe en lui-même indépendamment du choix d'un système de coordonnées particulier.

Articles d'analyse vectorielle
Objets d'étude
Champ vectoriel	Champ scalaire
Équation aux dérivées partielles
de Laplace	de Poisson
Opérateurs
Nabla	Gradient
Rotationnel	Divergence
Laplacien scalaire	Bilaplacien
Laplacien vectoriel	D'alembertien
Théorèmes
de Green	de Stokes
de Helmholtz	de flux-divergence
du gradient	du rotationnel

Exemples

Le cas le plus courant est la notion de coordonnées en géométrie, voir l'article Repérage dans le plan et dans l'espace : on choisit un point de repère appelé « origine », et trois « règles graduées » de directions distinctes qui ne sont pas dans le même plan (dans le plan, deux direction suffisent). Les coordonnées de ce point sont appelées « abscisse », « ordonnée » et « cote », et sont notées respectivement x, y et z. Voir aussi l'article Géométrie analytique.

En géographie, on associe une longitude et une latitude à des endroits géographiques ; c'est un système de coordonnées. Dans ce cas, la paramétrisation n'est pas unique aux pôles Nord et Sud.

Un exemple de système de coordonnées permet de décrire un point P dans l'espace euclidien par un n-uplet :

étant des nombres réels appelés coordonnées du point P.

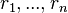
Si un sous-ensemble S d'un espace euclidien est appliqué de façon continue sur un autre espace topologique, cela définit les coordonnées de l'image de S. On peut parler de paramétrisation de l'image, puisque ce processus assigne des nombres aux points. La correspondance est unique seulement si l'application est bijective.

Systèmes courants

Quelques systèmes de coordonnées couramment utilisés :

• le système de coordonnées cartésiennes utilisé dans un espace vectoriel ou un espace affine de dimension finie.
• pour tout espace vectoriel de dimension finie et toute base, les coefficients des vecteurs exprimés dans cette base peuvent être utilisés comme coordonnées. Changer de base est une transformation de coordonnées, une transformation linéaire qui peut être définie par une matrice.
• le système de coordonnées curvilignes est une généralisation, basée sur des intersections de courbes.
• les systèmes de coordonnées polaires :
  • le système de coordonnées cylindriques représente un point dans l'espace par un angle, une distance à l'origine et une hauteur.
  • le système de coordonnées sphériques représente un point dans l'espace par deux angles et une distance à l'origine. Le système de coordonnées géographiques en est dérivé.
• des systèmes de coordonnées généralisées sont utilisés en mécanique lagrangienne.