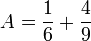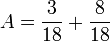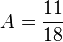Fraction (mathématiques) - Définition

Autres fractions

• fraction irréductible : fraction dans laquelle le numérateur et le dénominateur sont premiers entre eux.
• fraction unitaire : fraction dont le numérateur est égal à 1 et le dénominateur est un entier positif.
• fraction égyptienne : fraction qui est la somme de fractions unitaires, toutes distinctes.
• fraction décimale : fraction dont le dénominateur est une puissance de 10.
• fraction composée : fraction dont le numérateur et le dénominateur sont eux-mêmes des fractions :
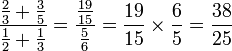
• fraction continue : fraction constituée à partir d'une suite d'entiers naturels (a₀,a₁,a₂,a₃,...,a_k,...) de la manière suivante
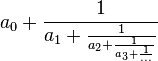
• fraction rationnelle : fraction constituée à partir de l'anneau des polynômes à coefficients dans .
• fonction rationnelle : quotient de deux fonctions polynômes
• Corps des fractions : corps construit à partir d'un anneau commutatif unitaire intègre et dans lequel on pourra effectuer des divisions.

Opérations sur les fractions

Addition et soustraction

Pour un dénominateur commun

Il suffit d'additionner ou de soustraire le numérateur de chaque fraction et de conserver le dénominateur commun.

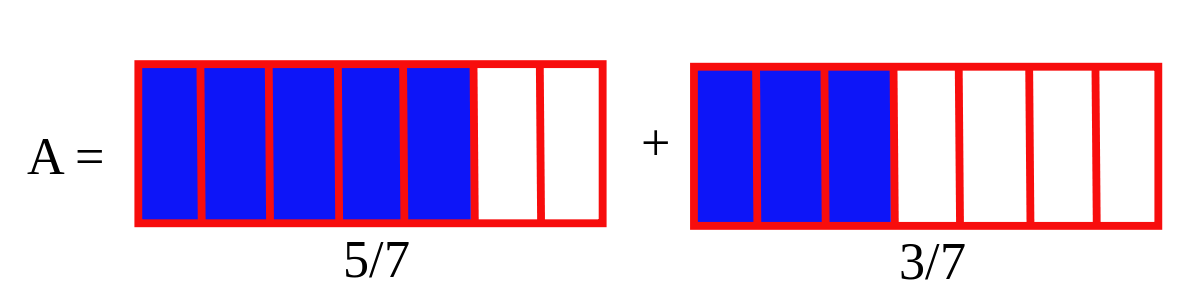
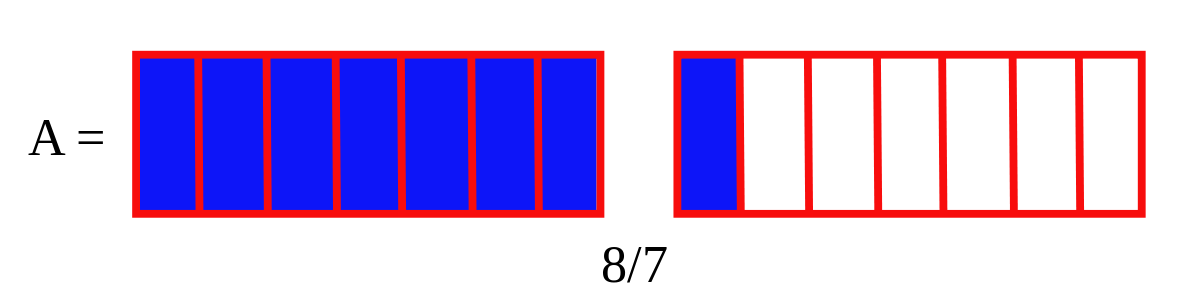
Exemple d'une somme :

Exemple d'une différence :

Pour un dénominateur différent

Avant d'effectuer l'opération, chaque fraction doit être transformée en une fraction équivalente dont le dénominateur leur soit commun.
Exemple :

Multiplication

La multiplication de deux fractions est simple à effectuer mais il n'est pas simple de comprendre pourquoi elle fonctionne ainsi.

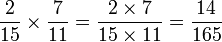
En voici une explication, basée sur une compréhension intuitive des fractions.

On peut comprendre sept onzièmes comme sept fois un onzième (voir les représentations graphiques ci-dessus) soit comme . Ainsi multiplier par revient à effectuer .
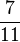
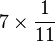
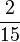
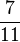
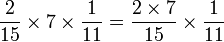
Mais multiplier par un onzième revient à diviser par 11, c'est-à-dire à multiplier le dénominateur par 11 (les parts sont 11 fois plus petites), soit : .

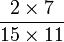
Problèmes historiques

1. J’ai trouvé une pierre mais je ne l’ai pas pesée. Après lui avoir ajouté un septième de son poids et avoir ajouté un onzième du résultat, j’ai pesé le tout et j’ai trouvé : 1 ma-na [unité de masse]. Quel était à l’origine le poids de la pierre? (problème babylonien, tablette YBC 4652, problème 7)
2. Un nombre augmenté de son septième donne 19. Quel est ce nombre ? (papyrus Rhind, problème 24)
3. Un nombre augmenté de son quart donne 15. Quel est ce nombre ? (papyrus Rhind, problème 26)
4. Supposons que l’on ait 9 tiges d’or jaune et 11 tiges d’argent blanc qui, à la pesée, ont des poids tout justes égaux. Si l’on échange entre elles une de leurs tiges, l’or devient plus léger de 13 liang [unité de masse]. On demande combien pèsent respectivement une tige d’or et une tige d’argent. (les Les neuf chapitres sur l'art mathématique, problème 7.17)
5. Une lance a la moitié et le tiers dans l’eau et neuf paumes à l’extérieur. Je te demande combien elle a de long. (problème médiéval)

Usage

Alors que les Français utilisent volontiers les chiffres à virgule, les Anglo-saxons préfèrent souvent exprimer les parties non entières par des fractions — sans doute en raison de la différence culturelle (songer par exemple à la popularité du système métrique et du système impérial dans les deux cultures). Par exemple, ils diront d'une personne qu'elle mesure 5 pieds ⅔ et non pas 5,67 pieds.