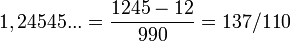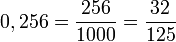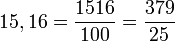Fraction (mathématiques) - Définition

Introduction

Une fraction, en mathématiques, est de manière naïve un certain nombre de parts considérés après la division d'un nombre entier en parts égales. Par exemple, la fraction désigne le quotient de 56 par 8. Elle est égale à 7 car 7×8 = 56. Dans cette fraction, 56 est appelé le numérateur et 8 le dénominateur.

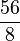
Les nombres que l'on peut représenter par des fractions de nombres entiers sont appelés nombres rationnels. L'ensemble des rationnels est noté .

Il existe une définition plus générale et plus abstraite des fractions. Si (A, +, .) est un anneau commutatif unitaire intègre, on peut créer le corps des fractions de A. Ses éléments se notent (par analogie aux fractions d'entiers relatifs) et possèdent les mêmes propriétés opératoires (somme, produit, simplification, ...) que les fractions de .

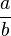
Sens usuel de la fraction

Définition de la fraction

Une fraction est une division non effectuée entre deux nombres entiers relatifs n et d . Elle est représentée comme suit :

n/d ou ⁿ⁄_d ou

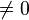
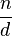
• Le nombre du haut s'appelle le numérateur............ n
• Le nombre du bas s'appelle le dénominateur......... d
• Le trait ou barre de fraction signifie que l'on divise le numérateur par le dénominateur.

Exemple : signifie que l'on divise 3 par 7; on prononce cette fraction « trois septièmes » et c'est pour cela que 3 est le numérateur parce qu'il indique un nombre de trois unités (les septièmes) alors que 7 est le dénominateur parce qu'il dénomme l'unité (le septième) avec laquelle on travaille.Si on mange les 3/7 d'une tarte, le numérateur 3 indique le nombre de parts que l'on mange alors que 7 indique le nombre total de parts, donc l'unité considérée...

On trouve aussi parfois la notation

n : d

ou encore

n ÷ d

les deux points remplaçant la barre de fraction (cette notation est à éviter). deux points (:) signifie que le resultat de la fraction sera un nombre entier,:- signifie qu'il sera décimal

Modélisation d'une fraction

Pour comprendre et établir les règles de maniements des fractions, il existe deux méthodes différentes. La première consiste à faire usage de la géométrie. La fraction représente une portion d'aire d'une figure géométrique ou d'une longueur d'un côté d'un polygone, souvent un triangle. Démontrer les lois régissant les fractions revient à faire de la géométrie et à mesurer des aires ou des longueurs. Cette démarche est décrite dans l'article Algèbre géométrique.

Une autre démarche est de nature purement algébrique. Les nombres rationnels sont construits de manière abstraite à partir de classes d'équivalence d'entiers. L'addition et la multiplication issues des nombres entiers sont compatibles avec la classe d'équivalence, ce qui équipe l'ensemble des fractions d'une addition et d'une multiplication naturelle. Cette construction permet d'établir les lois régissant le comportement des fractions.

La démarche choisie ici correspond à la première décrite et est purement géométrique. Les méthodes utilisées s'appliquent pour les fractions d'entiers. La géométrie offre une autre méthode, permettant de généraliser les résultats au cas de fractions de deux nombres réels positifs. Elle est décrite dans l'article Algèbre géométrique.

Représenter une fraction

Le but ici est de visualiser une fraction n/d

La fraction peut être représentée par un dessin. Bien souvent une forme géométrique que l'on divise en plusieurs parties.

Fractions dont n < d

1° Le dénominateur d indique le nombre de parties égales à dessiner dans la forme géométrique.
2° Le numérateur n indique le nombre de parties égales utilisées.
Exemple :
Choisissons un rectangle comme forme géométrique et la fraction ³⁄₄
Le dénominateur est 4 donc le rectangle sera divisé en 4 parties égales

Le numérateur est 3 donc seules 3 parties égales seront utilisées.

Autre possibilité :

Fractions dont n > d

Cette fraction sera équivalente au quotient de n/d, (qui représentera le nombre d'unité) suivi d'une fraction constituée par le reste de la division pour numérateur et d pour dénominateur.

Exemple : pour la fraction 7/3, la division entière donne 2, il reste 1.

Le quotient est 2 donc 2 unités, le reste 1 donc 2 1/3.

Il est impossible de représenter ce genre de fraction par un schéma unique, nous utiliserons dès lors plusieurs formes géométrique similaires:

Prendre une fraction d'une quantité

Pour prendre les ²⁄₃ de 750, on divise 750 par 3, puis on multiplie le résultat par 2:

750÷3 = 250 ; 250 × 2 = 500. Donc ²⁄₃ de 750 = 500

Prendre ^a⁄_b de c revient à diviser c par b et à multiplier le tout par a. Ou plus simplement, quand on connaît les règles de calcul sur les fractions, Prendre ^a⁄_b de c revient à multiplier ^a⁄_b par c. Plus généralement, on constate que le "de" est remplacé par une multiplication. Il en est de même quand on calcul 75% de c, on doit juste calculer 75% multiplié par c. En effet, 75% est une fraction : 75% = ⁷⁵⁄₁₀₀ = 0,75.

Fractions équivalentes

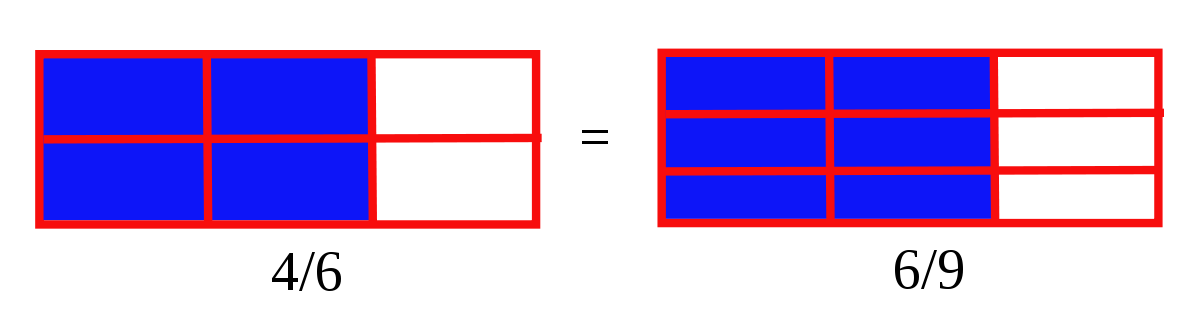
Si on multiplie, ou divise, le numérateur et le dénominateur d'une fraction par un même nombre, on obtient une fraction équivalente.

Exemple : (on a multiplié 2/3 par 2/2)

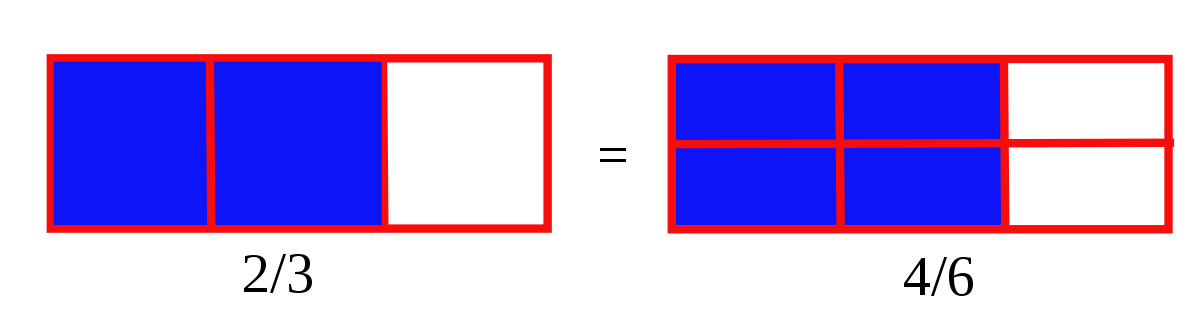
De manière générale, les fractions ⁿ⁄_d et ^n'⁄_d' sont équivalentes dès que n × d' = d × n'.

Exemple :

car (on appelle ces deux produits les produits en croix).

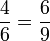
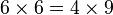
Certaines fractions peuvent être simplifiées, c'est-à-dire que n et d peuvent être divisés par un même nombre mais le plus grand possible. Ce nombre s'appelle le PGCD (plus grand commun diviseur) de n et d. Après réduction, la fraction est dite irréductible.

Pour effectuer certaines opérations entre fractions, tous les dénominateurs des fractions doivent être égaux. Pour ce faire, il faut remplacer chaque fraction par une fraction équivalente, en s'arrangeant pour que tous les dénominateurs soient identiques. Ce dénominateur sera le plus petit nombre possible qui soit divisible par chaque dénominateur. Ce nombre s'appelle le PPCM (plus petit commun multiple) des dénominateurs. L'opération s'appelle réduire au même dénominateur
Exemple :

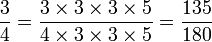
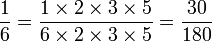
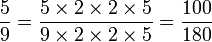
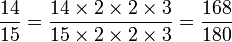
Comparaison de fractions

• Pour un même numérateur, plus le dénominateur est petit plus la fraction est grande.

Exemple :

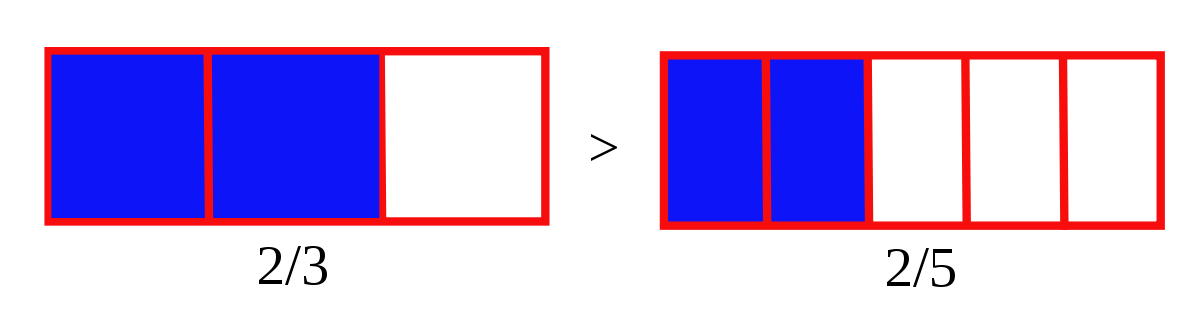
Le numérateur 2 est le même pour chaque fraction.

La comparaison des dénominateurs donne 3 < 5

• Pour un même dénominateur, plus le numérateur est grand, plus la fraction est grande :

Exemple :

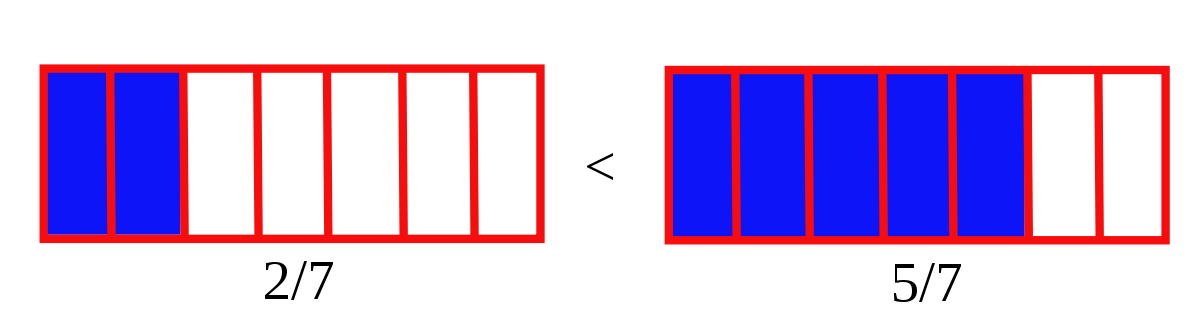
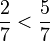
Le dénominateur 7 est le même pour chaque fraction.

La comparaison des numérateurs donne 2 < 5

• Si les numérateurs et les dénominateurs sont différents, on peut toujours réduire les fractions au même dénominateur et comparer alors les numérateurs : Comparaison de 1/4 et 2/5

1/4 =5/20 et 2/5 = 8/20. Or 5 < 8 donc 5/20 < 8/20 donc 1/4 < 2/5

Remarque : on peut aussi utiliser l'écriture décimale comme par exemple 1/4 = 0,25 et 2/5 = 0,4, 0,25 < 0,4 donc ¹⁄₄ < ²⁄₅.

Écriture décimale, écriture fractionnaire

Toute fraction possède un développement décimal fini ou illimité périodique qui s'obtient en posant la division de n par d.

1/4 = 0,25

2/3 = 0,666...(période 6)

17/7 = 2,428571428571...(période 428571)

Inversement, tout nombre décimal ou possédant un développement décimal périodique peut s'écrire sous forme de fraction.

Cas du nombre décimal

Il suffit de prendre comme numérateur le nombre décimal privé de sa virgule et comme dénominateur 10ⁿ où n est le nombre de chiffres après la virgule:

Cas du développement décimal illimité

On commence par se débarrasser de la partie entière: 3,4545... = 3 + 0,4545...

cas du développement décimal périodique simple

Un nombre périodique simple est un nombre décimal dans lequel la période commence immédiatement après la virgule.
0,666 ou 0,4545 ou 0,108108
Comme numérateur, il suffit d'utiliser la période tandis que le dénominateur sera composé d'autant de 9 qu'il y a de chiffres composant la période.
Exemple : 0,4545
Période 45 donc numérateur = 45
Période composée de deux chiffres donc dénominateur = 99
Fraction = 45/99 ou 5/11 par conséquent: 3,4545... = 3 + 5/11 = 38/11

Sinon : Posons x pour 0,4545454545...

100x=45,4545454545 donc 99x=45 donc x = 45/99

Cas du développement décimal périodique mixte

Un nombre décimal périodique mixte est un nombre décimal dans lequel la période ne commence pas immédiatement après la virgule.
0,8333 ou 0,14666
Pour trouver le numérateur de la fraction, il faut soustraire la valeur mixte de la valeur mixte suivie de la première période. Exemple : 0,36981981...
valeur mixte : 36
Valeur mixte suivie de la première période : 36981
Numérateur = 36981 - 36 = 36945
Quant au dénominateur, il sera composé d'autant de 9 qu'il y a de chiffres composant la période, suivis d'autant de zéros qu'il y a de chiffres après la virgule composant la valeur mixte.

Exemple 1 : dans la valeur 0,36981981, la période 981 est constituée de 3 chiffres donc le dénominateur sera constitué d'une série de trois 9 suivis de deux zéros puisque la valeur mixte 36 est composée de deux chiffres. Finalement nous aurons :
0,36981981 = 36945/99900 ou 821/2220

Exemple 2 :