Frustration géométrique - Définition
La liste des auteurs de cet article est disponible ici.
Bibliographie
- G. Toulouse, Comm.~Phys., 2 (1977) 115.
- J.F. Sadoc and R. Mosseri, "Geometrical Frustration "Cambridge Univ. Press(1999, reedited 2007)
- Sadoc JF, editor. Geometry in condensed matter physics. Singapore: World Scientific; 1990.
- H.S.M. Coxeter, Regular polytopes (Dover pub., 1973).
- D. Dai and M.-H. Whangbo, J. Chem. Phys., 121 (2004), 672
Frustration d'orientation
Le terme de frustration géométrique est aussi utilisé en physique de la matière condensée quand les propriétés géométriques du réseau cristallin interdisent l'existence d'un état fondamental unique, impliquant une entropie non nulle à 0 K. Un exemple de matériau frustré géométriquement est la glace d'eau, dont l'entropie au zéro absolu vaut environ 3,40 J/K/mole.
La frustration d'un système de spins en est un exemple important en magnétisme. Dans ce cas elle est due à l'orientation spatiale des spins incompatible avec la minimisation de l'énergie d'interaction voir verre de spins. Un exemple simple est décrit par la figure 1. Trois ions magnétiques en interactions antiferromagnétique (i.e. les spins tendent à pointer dans la direction opposée de ses voisins) sont placés aux coins d'un triangle. Les deux premiers spins étant anti-parallèles, le troisième est frustré car ses deux orientations (haut ou bas) donnent la même énergie - le troisième spin ne peut pas minimiser simultanément ses interactions avec les deux autres. Ainsi l'état fondamental est deux fois dégénéré.
Une frustration géométrique peut également survenir lorsque quatre spins sont placés sur un tétraèdre (Figure 2). Si les spins sont en interactions antiferromagnétiques, alors il n'est pas possible de réarranger les spins de telle sorte que toutes les interactions entre spins soient antiparallèles. Une fois encore le système est frustré.
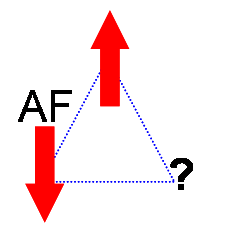
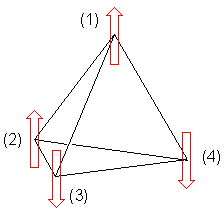
Une conséquence de la frustration géométrique est que le niveau de plus basse énergie est dégénéré.

















































