Frustration géométrique - Définition
La liste des auteurs de cet article est disponible ici.
De l'ordre local au remplissage global de l'espace
Expliquer de la stabilité d'un solide est une question centrale en physique de la matière condensée. Possible dans le cas des molécules, les calculs quantiques les plus précis montrent souvent une grande diversité pour les configurations atomiques de faible énergie. Du fait de leur taille macroscopique, et donc du nombre astronomique d'atomes mis en jeu, la même étude pour les solides impose que de nombreuses approximations soient faites pour calculer leur énergie de cohésion. Bien que, certains effets structuraux fins ne soient expliqués que par l'intervention de critères quantiques, il est toujours bien utile de pouvoir approximer l’énergie de cohésion comme une somme d'interactions de type classique, par exemple par des potentiels à deux ou plusieurs termes. Alors Il est souvent possible de proposer des règles locales, de nature chimique, qui mènent aux configurations de basse énergie et gouvernent l'ordre structurel ou chimique dans le système considéré. La frustration géométrique, concerne les cas où l'ordre local ne peut se propager librement dans tout l'espace. Cette définition suffisamment générale de la frustration ne se restreint pas qu’aux organisations atomique, ni même aux systèmes discrets. Ainsi, dans les cristaux liquides, si l'on passe à un modèle continu, il est alors possible de caractériser certains systèmes comme étant géométriquement frustrés : systèmes de molécules cholestériques chirales ou bien ensembles de bicouches d'amphiphiles entrent dans ce cadre. Une caractéristique commune à tous ces systèmes est que, même avec des règles locales simples, ils présentent une assez grande variété de réalisations structurales, souvent complexes. Cela rappelle un champ voisin de la physique, celui des systèmes de spins frustrés, dont l'étude du paysage énergétique tourmenté a fait l'objet de contributions nombreuses et profondes. Il n'est pas inutile de préciser pour autant la différence avec la frustration géométrique au sens stricte. Dans les systèmes de spins, ce n'est pas en général la localisation des spins dans l'espace qui peut varier, mais plutôt la variable interne, le spin lui-même, ou encore l'interaction entre ces spins. En conséquence, malgré une problématique commune, les méthodes d'investigation théorique diffèrent notablement d’un cas à l’autre. La frustration géométrique est un concept unificateur, qui joue un rôle important dans des domaines très différents de la matière condensée, depuis les agrégats et les amorphes jusqu'aux fluides complexes.
L’approche générale suit deux étapes. D'abord, relaxer la contrainte de remplissage de l'espace en permettant à celui-ci de se courber. Une structure idéale, non frustrée, est alors définie dans un espace courbe. Ensuite, des distorsions spécifiques sont appliquées à ce modèle idéal afin de pouvoir le plonger dans l'espace euclidien tridimensionnel. Cela permet de décrire la structure finale comme un mélange de régions ordonnées, où l'ordre local est semblable à celui du modèle idéal, et de défauts, qui proviennent de la projection. Parmi tous les défauts possibles, les lignes de disinclinaison jouent un rôle prépondérant.
Exemples bidimensionnels simples
Les exemples bidimensionnels sont utiles pour suivre le rôle de la compétition entre les règles et la géométrie locales et globale. Considérons un arrangement des disques identiques placés sur un plan (un modèle pour un hypothétique métal bidimensionnel) en supposant que l'interaction isotrope entre les disques tend localement à une organisation la plus dense possible. Le meilleur arrangement pour trois disques est trivialement un triangle équilatéral avec les centres de disque situés aux sommets du triangle. L'étude de la structure à grande distance peut être réduite à un pavage du plan par des triangles équilatéraux. Dans cet exemple de structure dite hexagonale. il y a compatibilité totale entre les règles locales et globales : le système est non frustré.
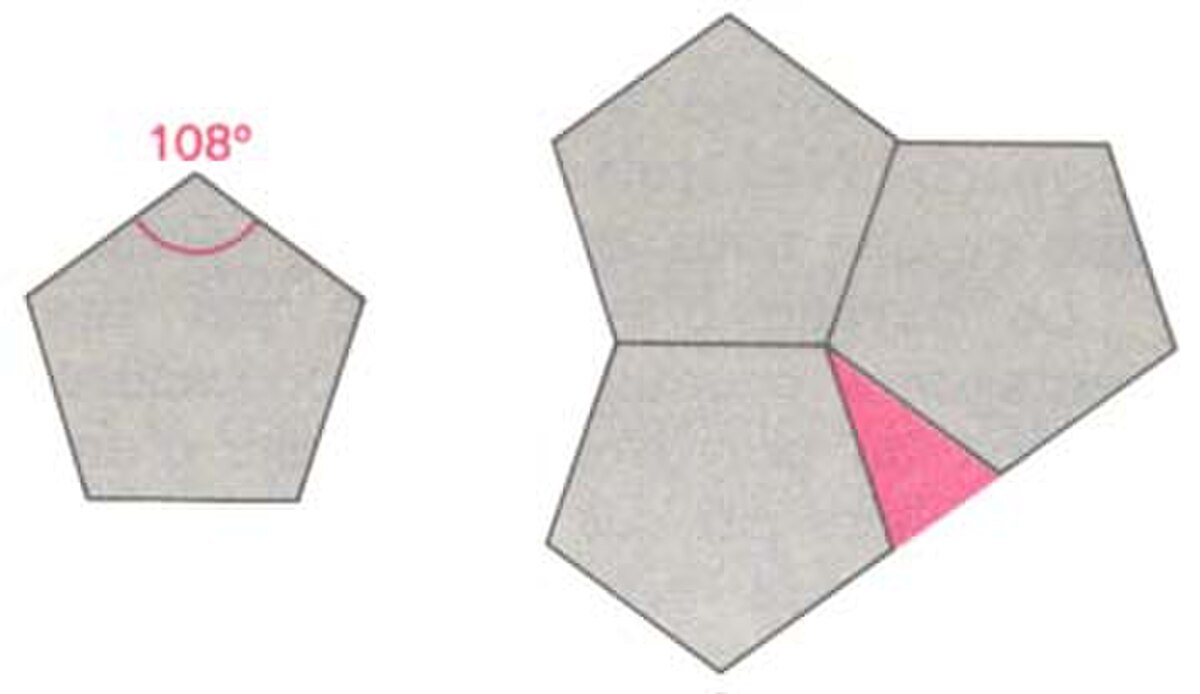
Dans un exemple opposé, l'énergie d'interaction est censée être minimum quand les atomes sont placés sur les sommets de pentagones réguliers. Toute tentative de propager sur une grande surface plane un pavage de ces pentagones partageant des côtés (liens atomiques) et des sommets (atomes) est impossible. C'est dû à l'impossibilité de paver le plan avec des pentagones réguliers, simplement parce que l'angle au sommet du pentagone régulier n’est pas sous multiple de 2π. Trois pentagones peuvent facilement être assemblés avec un sommet commun, mais un espace demeure entre deux arêtes. Ce genre d'anomalie est un exemple simple de « frustration géométrique ».
Il y a une façon de surmonter cette impossibilité, laissons la surface à paver libre de toute topologie et métrique, et étendons le pavage de façon à satisfaire strictement la règle d'interaction locale. On observe alors que la surface hérite de la topologie de la sphère et devient donc courbe. La structure finale, un dodécaèdre pentagonal, permet donc la propagation parfaite de l'ordre pentagonal. C'est un modèle idéal (sans défauts) pour le système considéré.
Structures denses tétraédriques
La stabilité des métaux peut être comprise avec une image très simplifiée de la liaison métallique ne gardant que l’aspect isotrope des interactions. Les structures apparaissent alors comme des empilements dense de sphères dures en contactes. En effet les structures simples cristallines des métaux sont souvent les structures denses cubique à faces centrées (f.c.c.) ou empilement hexagonal compact (h.c.p.). Dans une certaine mesure, les métaux amorphes et les quasi-cristaux peuvent également être modélisés par des empilement de sphères. Le problème de l'empilement de sphères dures peut être transformé en un problème d'empilement de tétraèdres réguliers car le tétraèdre régulier est la configuration la plus dense pour quatre sphères en contactes placées à ses sommets.L'ordre atomique local est bien représenté par un pavage de tétraèdres, menant à un ordre icosaèdre imparfait.
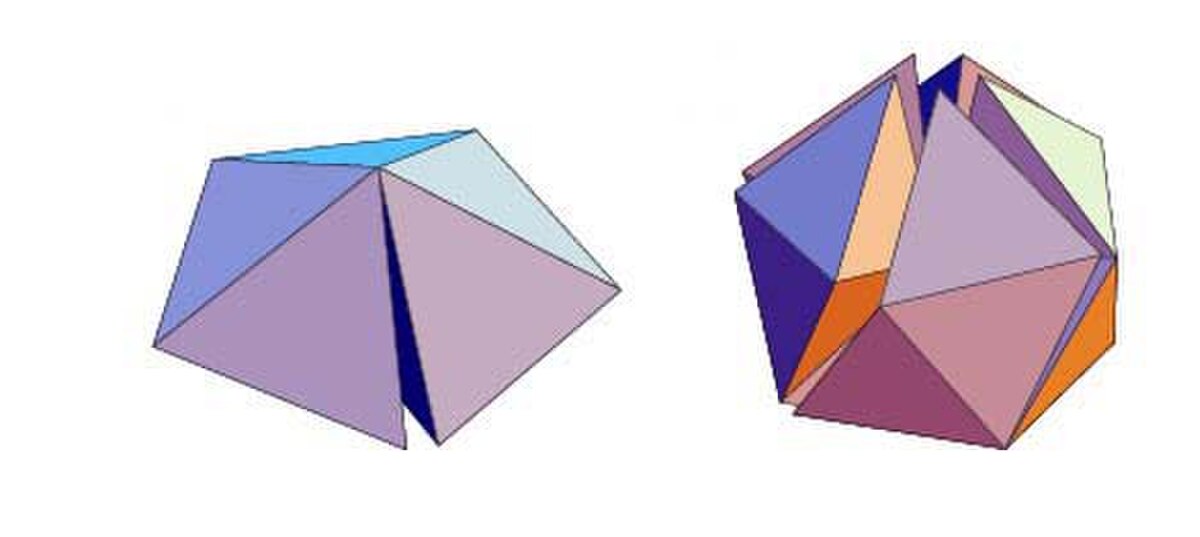
Le lecteur peut s'exercer à empiler des balles de ping-pong pour former un tétraèdre régulier et chercher alors à continuer en ne formant que des tétraèdres de façon à avoir une forte compacité. Très vite il apparaît que l’on obtient une solution incompatible avec les solutions cristallines cubique à faces centrées et hexagonale compacte. Une étape de la construction donne un agrégat de sept balles : deux balles axiales en contact, entourées de cinq autres, la forme extérieure étant une bi-pyramide pentagonale presque régulière. Mais il y a maintenant un réel problème de construction, similaire à celui rencontré avec le pavage pentagonal à deux dimensions. L'angle dièdre du tétraèdre n'est pas sous-multiple de 2π. En conséquence, il reste un petit interstice entre deux faces de tétraèdres voisins. En conséquence, il n'est pas possible de paver l'espace euclidien à 3 dimensions avec des tétraèdres réguliers. En fait la frustration a un caractère topologique : il est impossible de paver l'espace euclidien avec des tétraèdres quelconques, s'il est imposé que partout le même nombre de tétraèdres partagent une arête commune. En forçant la perfection de cet arrangement local on construit une structure non frustrée. Mais pour cela l'espace sous-jacent doit être courbé, afin de permettre aux configurations tétraédriques locales de se propager sans défauts dans tout l'espace. La structure idéale est alors un empilement régulier de 120 tétraèdres dans une hypersphère : le polytope{3,3,5}. Autour d'un sommet commun 20 tétraèdres forment un icosaèdre régulier.