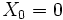Générateur congruentiel linéaire - Définition

Exemples

Algorithme	a	c	m	Remarques
RANDU	65539	0	231	Biaisé et fortement déconseillé
générateur de Robert Sedgewick	31415821	1	108	Intéressant mais déconseillé (essayer avec )
Standard minimal	16807	0	231-1

• RANDU défini par . Implanté sur les IBM System/370 et réputé mauvais par tous ceux qui ont à l'utiliser sérieusement
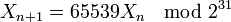
• Le générateur de Turbo Pascal défini par . On sait dans 1 cas sur 129 que X_{n + 1} > X_n, ce qui est un biais énorme pour une application scientifique. En plus comme 129 est de la forme 2^n + 1, les nombres produits ne sont pas si « aléatoires que ça » [cf. Knuth p.23].
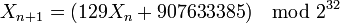
• Le générateur d'UNIX (dont le comité ANSI C a heureusement recommandé de ne conserver que les 16 bits de poids fort) :

. Même la documentation du Berkeley 4.2 admet que les bits de poids faible des nombres produits ne sont pas vraiment aléatoires.

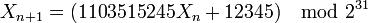
autres exemples

D. Knuth recense dans « Seminumerical Algorithms » un certain nombre de générateurs congruentiels linéaires de qualité. S'il n'est pas possible d'utiliser le Standard Minimal, on pourra essayer par exemple :

• (une suite cyclique de 256 nombres, est-ce encore du hasard ?)
•  : générateur de Knuth & Lewis
•  : générateur de Marsaglia au multiplicande remarquable, utilisé sur le VAX
•  : générateur de Lavaux & Jenssens
•  : générateur de Haynes

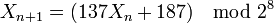
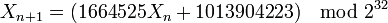
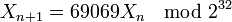
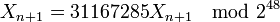
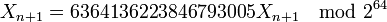
Dans tous ces cas, comme le modulant est une puissance de 2, les bits de poids faible des nombres produits ne sont pas eux très « aléatoires ». Il est par conséquent préférable de ne conserver que les poids forts (16 bits par exemple), comme le fait le générateur de Borland C++ par exemple :

• et on sort X_{n + 1} > > 16

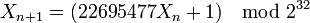
Ce faisant, la période du générateur reste la même mais on ne va produire que des nombres compris entre 0 et 65535, chacun se retrouvant 65536 fois dans la suite.

Tests statistiques

Comme tous les générateurs de nombres pseudo-aléatoires, le générateur congruentiel linéaire doit être soumis à une série de tests avant d’être homologué.

Le plus connu d’entre eux, le test de fréquence n'est généralement pas un problème pour un générateur congruentiel linéaire de période maximale, mais il existe bien d'autres tests. Test des séries, Gap test, Run test, ...
L'un des plus discriminant, car aucun générateur congruentiel linéaire démontré mauvais ne l’a réussi, étant le test spectral.