Géométrie projective - Définition

Transformation projective ou homographie

Les transformations projectives ou homographies sont des transformations étudiées en géométrie projective. Elles s'obtiennent comme composée d'un nombre fini de projections centrales. Elles décrivent ce qui arrive aux positions observées de différents objets quand l'œil de l'observateur change de place. Les transformations projectives ne conservent par toujours les distances ni les angles mais conservent les propriétés d'incidence et le birapport - deux propriétés importantes en géométrie projective. On trouve des transformations projectives sur des droites, dans des plans et dans l'espace.

Propriété fondamentale : En dimension finie, une transformation projective est entièrement déterminée par l'image d'un repère de l'espace projectif.

Définition analytique d'une homographie

Soient 2 espaces projectifs et associés respectivement aux espaces vectoriels et . On désigne par et les projections canoniques de (resp. ) sur (resp. ).

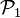
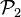
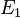
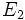
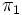
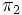
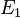
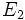
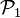
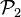
On peut alors effectuer un « passage au quotient » des applications linéaires injectives de dans . Une telle application linéaire étant donnée on peut définir une application de dans transformant le point en désignant un représentant de . Naturellement pour que cette définition soit cohérente, nous devons vérifier qu'elle ne dépend pas du représentant choisi, ce qui est immédiat vu la linéarité de et la définition de .

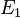
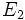
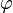
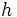
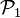
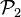
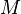
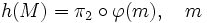
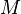
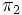
L'application est l'homographie associée à . Elle est de façon plus concise définie par l'égalité: .

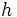
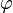
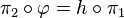
On peut aussi parler plus généralement d'application projective, en n'exigeant pas l'injectivité de l'application linéaire initiale ; le même procédé de passage au quotient fournira une application définie seulement sur une partie de  : , et à valeurs dans . On ne parlera pas alors d'homographie.

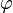
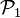
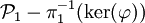
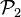
Il existe une infinité d'applications linéaires associées à une homographie mais ces applications linéaires forment une droite vectorielle de puisque entraîne .

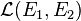
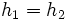
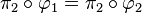
En dimensions finies p,n, si on dispose d'un système de coordonnées homogènes, une homographie pourra être définie par une classe de matrices non nulles de format (n+1)*(p+1) toutes multiples de l'une d'elles. A étant une de ces matrices et X une matrice-colonnes de coordonnées homogènes de , AX sera matrice colonne de coordonnées homogènes de (tout ceci étant donc défini à un facteur près).

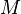
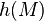
Exemple et discussion (géométrie plane).

Nous prenons pour et l'espace . est le plan projectif . Envisageons une homographie définie par la matrice 3*3 A que nous supposons diagonalisable. On peut donc calculer les coordonnées homogènes des transformés de tout point.

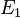
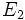
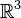
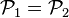
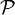
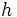
Les 3 directions propres sont indépendantes et définissent 3 points invariants par de . Ces 3 points ont respectivement comme matrices-colonne de coordonnées homogènes X₁,X₂,X₃ (vecteurs propres de la matrice, à un facteur non nul près).

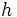
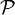
Inversement la connaissance de ces 3 points invariants détermine-t-elle l'homographie, c'est-à-dire A, à un facteur près ? Pour cela il faudrait pouvoir calculer les valeurs propres de A (à un facteur de proportionnalité près toujours). Or on n'a évidemment aucun moyen pour cela en ne connaissant que les directions propres.

Par contre si on se donne par exemple le transformé du point de coordonnées homogènes X₁ + X₂ + X₃ en le point de coordonnées homogènes Y, on aura en désignant par λ₁,λ₂,λ₃ les valeurs propres de A: quelconque non nul, ce qui permet bien de calculer en résolvant le système les valeurs propres à un coefficient de proportionnalité près.

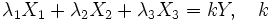
Les 4 points (les 3 points invariants plus le 4^e défini ci-dessus) définissent un repère projectif (voir plus haut) et la connaissance de la transformation de ce repère projectif détermine entièrement l'homographie.

Exemple d'homographie

Les transformations par polaires réciproques.