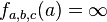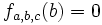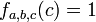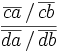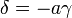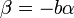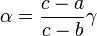Géométrie projective - Définition
La liste des auteurs de cet article est disponible ici.
Birapport sur une droite projective
Si



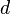
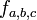
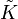
On appelle birapport de



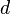
![[a:b:c:d]\,](https://static.techno-science.net/illustration/Definitions/autres/b/bb35a69f72c0b7509169c36addd5cd2a_bc710bcdb1476949f44ed4ea7cdb8924.png)
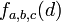
Si



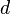
L'homographie
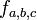
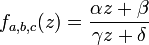
-
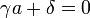

-
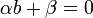
-
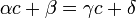
soit encore
En prenant
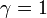
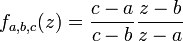
Cette définition du birapport rend aisée la preuve du résultat suivant : les homographies conservent le birapport. Plus précisément :
Invariance projective du birapport — a,b,c et d sont quatre point d'une droite projective D (a, b, c distincts) et e, f, g et h quatre points sur une droite D' (e, f, g distincts) alors il existe une homographie envoyant le premier quadruplet sur le second si et seulement si les birapports [a:b:c:d] et [e:f:g:h] sont égaux.
Dualité
Si E est un K-espace vectoriel de dimension finie n, son dual E* est aussi un K-espace vectoriel de dimension n. On peut donc associer à l'espace projectif P(E), son dual P(E*). Une droite de P(E*) correspondra à un faisceau d'hyperplans dans P(E). Le passage au dual permet d'inverser un grand nombre de propriétés géométriques.
Topologie
- Voir l'article détaillé : Topologie en géométrie projective.
Si E est un espace vectoriel sur


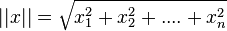
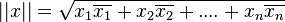
Cette topologie permet de définir sur l'espace quotient
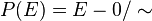
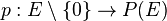
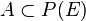
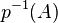
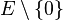
On montre que
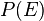
On munira donc l'espace projectif P(E) de cette topologie. Elle permet de parler d'homéomorphisme et de remarquer, par exemple, que la droite projective réelle est homéomorphe à un cercle, la droite projective complexe étant homéomorphe à une sphère (voir l'article sphère de Riemann pour un homéomorphisme explicite).
Utilité
- La géométrie projective a permis de simplifier grandement des théorèmes de géométrie plane comme le théorème de Pappus ou le théorème de Desargues.
- Si l'espace projectif, comparé à l'espace usuel, c'est-à-dire l'espace affine, peut sembler être un objet plus compliqué, il est indéniable que pour de nombreuses situations, l'espace projectif est le bon cadre pour travailler. Pour donner un exemple, si C et C' sont deux courbes planes (complexes) de degré respectif d et d' alors, si on voit ces courbes comme des sous-variétés du plan affine, le théorème de Bezout dit que le nombre de points d'intersection entre C et C' est toujours inférieur ou égal à dd'. En revanche, si on voit ces courbes comme des sous-variétés du plan projectif, alors le théorème dit que le nombre de points d'intersection (comptés avec multiplicité) est égal à dd'. Il y a de nombreuses autres situations où les théorèmes s'énoncent sous un forme plus belle en géométrie projective.
- Enfin, avec le développement de la représentation en 2D d'objets en 3D, la géométrie projective a montré la puissance des outils de dessin assisté par ordinateur qui ont été mis en place.