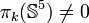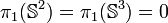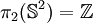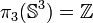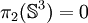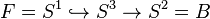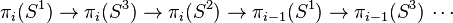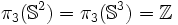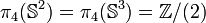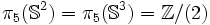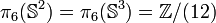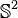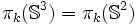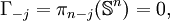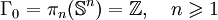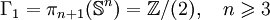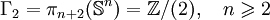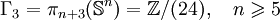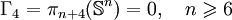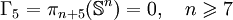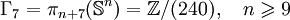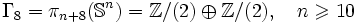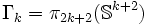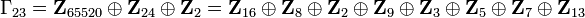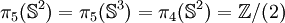Samedi 14 Décembre 2024
Rechercher 🔍

Groupes d'homotopie des sphères - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Propriétés générales - Dimensions 2 et 3 - Dimension 1 - Applications - Théorie générale - Références en français - Généralisation en géométrie algébrique

Introduction

En mathématiques, et plus spécifiquement en topologie algébrique, les groupes d'homotopie des sphères sont des invariants qui décrivent, en termes algébriques, comment des sphères de dimensions égales ou différentes peuvent s'enrouler l'une sur l'autre.

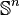
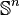
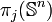
Le groupe d'homotopie d'ordre j de la sphère de dimension n, \mathbb{S}^n , est l'ensemble, noté \pi_{j}(\mathbb{S}^n) =[\mathbb{S}^j\to\mathbb{S}^n] , des classes d'homotopie d'applications qui envoient un point fixé de la sphère \mathbb{S}^j sur un point fixé de la sphère \mathbb{S}^n . Cet ensemble (pour j et n fixés), noté \pi_{j}(\mathbb{S}^n) , peut être muni d'une structure de groupe abélien.

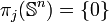
Si j < n, ce groupe est réduit à un seul élément : \pi_{j}(\mathbb{S}^n)=\{0\} .

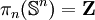
Si j = n, ce groupe est monogène infini (c'est-à-dire infini et engendré par un seul élément) : \pi_{n}(\mathbb{S}^n)=\mathbf{Z} .

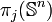
Si j > n, le groupe \pi_{j}(\mathbb{S}^n) est soit un groupe fini, soit la somme d'un groupe fini et d'un groupe infini monogène.

La suite spectrale de Serre fut inventée pour calculer les groupes d'homotopie des sphères, mais aucune liste complète de ces groupes n'est connue. Pour calculer ces groupes, on utilise aussi les fibrations de Hopf et la technique des variétés équipées (framed en anglais) qui provient de la théorie du cobordisme.

Propriétés générales

On peut obtenir quelques résultats vrais en toute dimension :

  • Les groupes d'homotopie des sphères sont des groupes abéliens de type fini (avec un nombre fini de générateurs).
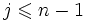
  • pour \quad j\leqslant n-1
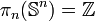
  • \pi_n(\mathbb{S}^n)=\mathbb{Z}

Dimensions 2 et 3

Les sphères de dimension au moins deux sont simplement connexes donc :

\pi_1(\mathbb{S}^2)=\pi_1(\mathbb{S}^3)=0

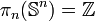
En toute dimension, on a : \pi_n(\mathbb{S}^n)=\mathbb{Z} , donc :

\pi_2(\mathbb{S}^2)=\mathbb{Z}
\pi_3(\mathbb{S}^3)=\mathbb{Z}

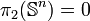
En toute dimension supérieure ou égale à 3, on a : \pi_2(\mathbb{S}^n)=0 , donc

\pi_2(\mathbb{S}^3)=0

En dimension 2 et 3, la fibration de Hopf

F=S^1\hookrightarrow S^3\rightarrow S^2=B \,\!

donne lieu à une suite exacte d'homotopie,

\pi_i(S^1)\to \pi_i(S^3) \to \pi_i(S^2) \to \pi_{i-1}(S^1)\to \pi_{i-1}(S^3)\, \cdots

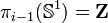
Lorsque i=2, et \pi_{i-1}(\mathbb{S}^1)=\mathbf Z

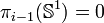
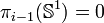
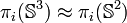
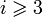
Lorsque i>2 , \pi_{i-1}(\mathbb{S}^1)=0 et \pi_{i-1}(\mathbb{S}^1)=0 , on a donc un isomorphisme :

\pi_i(\mathbb{S}^3)\approx\pi_i(\mathbb{S}^2) pour i\geqslant 3 ,

donc

\pi_3(\mathbb{S}^2)=\pi_3(\mathbb{S}^3)=\mathbb{Z}

Pour les groupes d'homotopie supérieurs, d'autres techniques donnent les résultats suivants :

  • \pi_4(\mathbb{S}^2)=\pi_4(\mathbb{S}^3)=\mathbb{Z}/(2)
  • \pi_5(\mathbb{S}^2)=\pi_5(\mathbb{S}^3)=\mathbb{Z}/(2)
  • \pi_6(\mathbb{S}^2)=\pi_6(\mathbb{S}^3)=\mathbb{Z}/(12)
Groupes d'homotopie de \mathbb{S}^3 et \mathbb{S}^2
k 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
\pi_k(\mathbb{S}^3)=\pi_k(\mathbb{S}^2) Z Z2 Z12 Z2 Z3 Z15 Z2 Z22 Z12×Z2 Z84×Z22 Z22 Z6 Z30 Z2×Z6 Z22×Z12 Z22×Z132

Dimension 1

En dimension 1, on a:

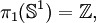
  • \pi_1(\mathbb{S}^1)=\mathbb{Z},
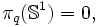
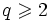
  • \pi_q(\mathbb{S}^1)=0,\quad pour \quad q\geqslant 2

Applications

  • Pour les applications du groupe fondamental (n=1), voir l'article Groupe fondamental.
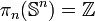
  • Le fait que \pi_{n}(\mathbb{S}^{n})=\mathbb{Z} implique le théorème de Brouwer qui affirme que toute application continue de la boule (de dimension >1) dans elle-même a un point fixe.

Ce groupe permet de définir le degré de Brouwer d'une application de la sphère dans elle-même.

  • Les groupes d'homotopie stable sont importants en théorie des singularités.
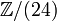
  • Le fait que le 3e groupe d'homotopie stable est \mathbb{Z}/(24) implique le théorème de Rokhlin qui affirme que la signature d'une variété spinorielle de dimension 4 est divisible par 16.
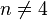
  • Les groupes d'homotopie stable servent à décrire les groupes de h-cobordisme des homotopies orientées de sphères, qui pour n\neq 4 est le groupe des sphères exotiques orientées de dimension n.
  • Les groupes d'homotopie des sphères sont liés aux classes de bordisme des variétés.
  • Ils permettent également de calculer les groupes d'homotopie des fibrés, des groupes de Lie et des espaces symétriques.

Théorie générale

Table

Calculer les groupes d'homotopie des sphères est difficile et les résultats sont compliqués. La table suivante donne une idée de la complexité :

π1 π2 π3 π4 π5 π6 π7 π8 π9 π10 π11 π12 π13 π14 π15 π16
S1 Z 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
S2 0 Z Z Z2 Z2 Z12 Z2 Z2 Z3 Z15 Z2 Z22 Z12×Z2 Z84×Z22 Z22 Z6
S3 0 0 Z Z2 Z2
S4 0 0 0 Z Z2 Z2 Z×Z12 Z22 Z22 Z24×Z3 Z15 Z2 Z23 Z120×Z12×Z2 Z84×Z25 Z26
S5 0 0 0 0 Z Z2 Z2 Z24 Z2 Z2 Z2 Z30 Z2 Z23 Z72×Z2 Z504×Z22
S6 0 0 0 0 0 Z Z2 Z2 Z24 0 Z Z2 Z60 Z24×Z2 Z23 Z72×Z2
S7 0 0 0 0 0 0 Z Z2 Z2 Z24 0 0 Z2 Z120 Z23 Z24
S8 0 0 0 0 0 0 0 Z Z2 Z2 Z24 0 0 Z2 Z×Z120 Z24
S9 0 0 0 0 0 0 0 0 Z Z2 Z2 Z24 0 0 Z2 Z240

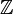
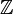
Les entrées de la table sont soit le groupe trivial 0, soir le groupe monogène infini \mathbb Z , soit les groupes abéliens finis ou encore (cases rouges) le produit de tels groupes finis abéliens et de \mathbb Z .

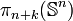
Les tables de groupes d'homotopies sont plus facilement organisées en présentant \pi_{n+k}({\mathbb{S}}^n) en fonction de n et de k :

πn πn+1 πn+2 πn+3 πn+4 πn+5 πn+6 πn+7 πn+8 πn+9 πn+10 πn+11 πn+12 πn+13
S1 Z 0 0 0 0 0 0 0 0 0 0 0 0 0
S2 Z Z Z2 Z2 Z12 Z2 Z2 Z3 Z15 Z2 Z22 Z12×Z2 Z84×Z22 Z22
S3 Z Z2 Z2 Z12 Z2 Z2 Z3 Z15 Z2 Z22 Z12×Z2 Z84×Z22 Z22 Z6
S4 Z Z2 Z2 Z×Z12 Z22 Z22 Z24×Z3 Z15 Z2 Z23 Z120×Z12×Z2 Z84×Z25 Z26 Z24×Z6×Z2
S5 Z Z2 Z2 Z24 Z2 Z2 Z2 Z30 Z2 Z23 Z72×Z2 Z504×Z22 Z23 Z6×Z2
S6 Z Z2 Z2 Z24 0 Z Z2 Z60 Z24×Z2 Z23 Z72×Z2 Z504×Z4 Z240 Z6
S7 Z Z2 Z2 Z24 0 0 Z2 Z120 Z23 Z24 Z24×Z2 Z504×Z2 0 Z6
S8 Z Z2 Z2 Z24 0 0 Z2 Z×Z120 Z24 Z25 Z242×Z2 Z504×Z2 0 Z6×Z2
S9 Z Z2 Z2 Z24 0 0 Z2 Z240 Z23 Z24 Z24×Z2 Z504×Z2 0 Z6
S10 Z Z2 Z2 Z24 0 0 Z2 Z240 Z22 Z×Z23 Z12×Z2 Z504 Z12 Z6
S11 Z Z2 Z2 Z24 0 0 Z2 Z240 Z22 Z23 Z6×Z2 Z504 Z22 Z6×Z2
S12 Z Z2 Z2 Z24 0 0 Z2 Z240 Z22 Z23 Z6 Z×Z504 Z2 Z6×Z2
S13 Z Z2 Z2 Z24 0 0 Z2 Z240 Z22 Z23 Z6 Z504 0 Z6
S14 Z Z2 Z2 Z24 0 0 Z2 Z240 Z22 Z23 Z6 Z504 0 Z×Z3
S14 Z Z2 Z2 Z24 0 0 Z2 Z240 Z22 Z23 Z6 Z504 0 Z3
S14 Z Z2 Z2 Z24 0 0 Z2 Z240 Z22 Z23 Z6 Z504 0 Z3
S14 Z Z2 Z2 Z24 0 0 Z2 Z240 Z22 Z23 Z6 Z504 0 Z3

Stabilité en grandes dimensions

Pour les dimensions supérieures, on a:

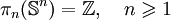
  • \pi_{n}(\mathbb{S}^{n})=\mathbb{Z},\quad n\geqslant 1 (première colonne du tableau précédent)
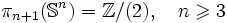
  • \pi_{n+1}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 3 (deuxième colonne du tableau précédent)
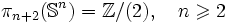
  • \pi_{n+2}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 2 (troisième colonne du tableau précédent)

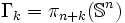
Comme il peut être conjecturé, il s'avère que \Gamma_k=\pi_{n+k}(\mathbb{S}^{n}) est indépendant de n pour n suffisamment grand. Ce phénomène est connu sous le nom de stabilité. Il résulte du théorème de Freudenthal suivant :

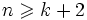
  • Le morphisme de suspension est un isomorphisme pour n\geqslant k+2
  • et un épimorphisme (morphisme surjectif) pour n = k + 1.

Liste des groupes d'homotopie stable

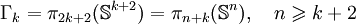
Les premiers groupes stables \Gamma_k=\pi_{2k+2}(\mathbb{S}^{k+2})=\pi_{n+k}(\mathbb{S}^{n}),\quad n\geqslant k+2 sont les suivants :

  • \Gamma_{-j}=\pi_{n-j}(\mathbb{S}^{n})=0,
  • \Gamma_0=\pi_{n}(\mathbb{S}^{n})=\mathbb{Z},\quad n\geqslant 1
  • \Gamma_1=\pi_{n+1}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 3
  • \Gamma_2=\pi_{n+2}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 2
  • \Gamma_3=\pi_{n+3}(\mathbb{S}^{n})=\mathbb{Z}/(24),\quad n\geqslant 5
  • \Gamma_4=\pi_{n+4}(\mathbb{S}^{n})=0,\quad n\geqslant 6
  • \Gamma_5=\pi_{n+5}(\mathbb{S}^{n})=0,\quad n\geqslant 7
  • \Gamma_6=\pi_{n+6}(\mathbb{S}^{n})=\mathbb{Z}/(2),\quad n\geqslant 5
  • \Gamma_7=\pi_{n+7}(\mathbb{S}^{n})=\mathbb{Z}/(240),\quad n\geqslant 9
  • \Gamma_8=\pi_{n+8}(\mathbb{S}^{n})=\mathbb{Z}/(2)\oplus\mathbb{Z}/(2),\quad n\geqslant 10

Les groupes d'homotopie stable sont finis sauf pour k = 0.

Groupes d'homotopie stable \ \Gamma_k=\pi_{2k+2}(\mathbb{S}^{k+2}) avec k inférieur à 23
k 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
Γk Z Z2 Z2 Z24 0 0 Z2 'Z240 Z22 Z23 Z6 Z504 0 Z3 Z22 Z480⊕ Z2 Z22 Z24 Z8⊕Z2 Z264⊕ Z2 Z24 Z22 Z22

À partir de k = 23, la décomposition de Γk se complique, par exemple :

\Gamma_{23}=\mathbf{Z}_{65520}\oplus\mathbf{Z}_{24}\oplus\mathbf{Z}_{2}=\mathbf{Z}_{16}\oplus\mathbf{Z}_{8}\oplus\mathbf{Z}_{2}\oplus\mathbf{Z}_{9}\oplus\mathbf{Z}_{3}\oplus\mathbf{Z}_{5}\oplus\mathbf{Z}_{7}\oplus\mathbf{Z}_{13}
Groupes d'homotopie stable \ \Gamma_k=\pi_{2k+2}(\mathbb{S}^{k+2}) avec k inférieur à 54
k 0 1 2 3 4 5 6 7
Γk Z Z2 Z2 Z24=Z8⊕Z3 0 0 Z2 Z240=Z16⊕Z3⊕Z5
k 8 9 10 11 12 13 14 15
Γk Z22 Z23 Z6=Z2⊕Z3 Z504=Z8⊕Z9⊕Z7 0 Z3 Z22 Z480⊕Z2=Z32⊕Z2⊕Z3⊕Z5
k 16 17 18 19 20 21 22 23
Γk Z22 Z24 Z8⊕Z2 Z264⊕Z2
=Z8⊕Z2⊕Z3⊕Z11		 Z24 Z22 Z22 Z16⊕Z8⊕Z2 ⊕Z9⊕Z3
⊕Z5⊕Z7⊕Z13
k 24 25 26 27 28 29 30 31
Γk Z22 Z22 Z22⊕Z3 Z24=Z8⊕Z3 Z2 Z3 Z6=Z2⊕Z3

Z64⊕Z22⊕Z3 ⊕Z5⊕Z17
k 32 33 34 35 36 37 38 39
Γk Z24 Z25 Z4⊕Z23 Z8⊕Z22⊕Z27
⊕Z7⊕Z19		 Z6=Z2⊕Z3 Z22⊕Z3 Z2⊕Z60=
Z2⊕Z4⊕Z3⊕Z5

Z16⊕Z25⊕Z32⊕Z25⊕Z11
k 40 41 42 43 44 45 46 47
Γk Z25⊕Z4⊕Z3 Z25 Z8⊕Z22⊕Z3 Z552
=Z8⊕Z3⊕Z23		 Z8 Z16⊕Z23
⊕Z9⊕Z5		 Z24⊕Z3

Z32⊕Z4⊕Z23 ⊕Z9⊕Z3
⊕Z5⊕Z7⊕Z13
k 48 49 50 51 52 53 54 55
Γk Z24⊕Z4 Z22⊕Z3 Z3⊕Z23 Z8⊕Z4⊕Z22⊕Z3 Z23⊕Z3 Z23

p-composantes des groupes d'homotopie stable

Voir l'article Groupe abélien de type fini pour la classification des groupes abéliens finis et la notion de p-composante.

La table précédente incite à s'intéresser à la classe de congruence modulo 4 de k, si p est un nombre premier supérieur ou égal à 7 :

  • Si k est pair ou congru à 1 modulo 4, la p-composante de Γk est 0 (quel que soit p >= 7 premier).
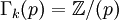
  • Si k est congru à 3 (ou -1) modulo 4, la p-composante de Γk est cyclique et d'ordre p ( \Gamma_k(p)=\mathbb{Z}/(p) ) si (p-1)/2 divise (k+1)/4, sinon elle est nulle (0).

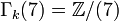
Par exemple \Gamma_k(7)=\mathbb{Z}/(7) si k = 12n − 1 et Γk(7) = 0 sinon.

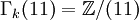
\Gamma_k(11)=\mathbb{Z}/(11) si k = 20n − 1 et Γk(11) = 0 sinon.

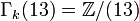
\Gamma_k(13)=\mathbb{Z}/(13) si k = 24n − 1 et Γk(13) = 0 sinon.

La complexité réside essentiellement dans les 2-, 3- et 5- composantes du groupe Γk.

Groupes d'homotopie non stables

Les premiers groupes non stables sont les suivants :

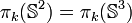
  • En dimension 2 et 3 ( \pi_k(\mathbb{S}^2)=\pi_k(\mathbb{S}^3) ) :
    • \pi_3(\mathbb{S}^2)=\pi_3(\mathbb{S}^3)=\mathbb{Z}
    • \pi_5(\mathbb{S}^2)=\pi_5(\mathbb{S}^3)=\pi_4(\mathbb{S}^2)=\mathbb{Z}/(2)
    • \pi_6(\mathbb{S}^2)=\pi_6(\mathbb{S}^3)=\mathbb{Z}/(12)
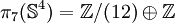
  • En dimension 4 : \pi_7(\mathbb{S}^4)=\mathbb{Z}/(12)\oplus\mathbb{Z}

Groupes d'homotopie infinis

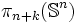
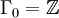
Les groupes d'homotopie stable \pi_{n+k}(\mathbb{S}^{n}) sont finis sauf pour k = 0 ( \Gamma_0=\mathbb{Z} ).

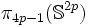
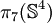
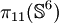
Les groupes d'homotopie instables sont finis sauf les groupes \pi_{4p-1}(\mathbb{S}^{2p}) . Ces derniers (, \pi_{7}(\mathbb{S}^{4}) , \pi_{11}(\mathbb{S}^{6}) , ...) sont isomorphes à la somme directe de \mathbb{Z} et d'un groupe fini.

Groupes d'homotopie non nuls

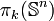
On sait que si n>1 il y a une infinité de groupes \pi_{k}(\mathbb{S}^{n}) qui sont non nuls (ce sont des résultats de Jean-Pierre Serre).

On sait aussi que \pi_k(\mathbb{S}^{5})\neq 0 pour tout k>4 (M.L. Curtis).

Références en français
- Introduction - Propriétés générales - Dimensions 2 et 3 - Dimension 1 - Applications - Théorie générale - Références en français - Généralisation en géométrie algébrique
miniature
Des particules de lumière "filmés" dans leur déplacement 🎬
miniature
Montre moi tes mains, je te dirai quel buveur d'alcool tu es 🍺
miniature
Ces papillons interprètent les "cris" des plantes pour choisir où pondre 🦋
miniature
3
Le nombre d'articles scientifiques rétractés est en hausse ❌
miniature
Une nouvelle manière de lire les mémoires magnétiques 🧲
miniature
2
Vous êtes né avant 1986 ? Voici pourquoi vous risquez de développer des troubles psychiques ⚠️
miniature
Ce nouveau modèle relie matière noire et inflation cosmique 🌀
miniature
Ils ont rendu ce bois bioluminescent: vers un nouveau mode d'éclairage ? 💡
miniature
Des mouches dans la station spatiale chinoise Tiangong 🛰️
miniature
Cette main-robot nanométrique est capable de saisir des virus (exemple avec la COVID-19) 🖐️
miniature
1
Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟
miniature
Cette astuce simple réduit la consommation d'alcool... des femmes 🍷
miniature
Découverte: la lumière transforme un isolant en métal 💡
miniature
1
Cet aliment à bannir nourrit les cancers 🍽️
miniature
Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️
miniature
Découverte d'une chimie des océans refroidissant le climat 🌊
miniature
Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭
miniature
Le rôle surprenant de la grossesse contre la grippe A 🦠
miniature
Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️
miniature
Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋
miniature
Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬
miniature
Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️
miniature
1
Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️
miniature
Ce nouveau type de moteur repousse les limites du vol supersonique ✈️
miniature
Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠
miniature
Une super-Terre entre Mars et Jupiter ? 🌎
miniature
Découverte impressionnante d'un fossile de crocodile géant 🐊
miniature
1
Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡
miniature
1
Un virage technologique révèle l'impact du diabète gestationnel 🩺
miniature
Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼
miniature
1
Ce fin gilet robotisé soulage les tâches répétitives 🦾
miniature
Les équations d'Einstein invalidées ? 👀
miniature
Ce tatouage électronique se connecte à votre cerveau 🧠
miniature
Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️
miniature
Des plats au bœuf... sans bœuf ? 🥩
miniature
2
Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍
miniature
Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️
miniature
Découverte: d'autres univers plus propices à la vie que le notre 👽
miniature
Ces sons urbains qui minent notre santé mentale 🚗
miniature
La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥
miniature
Des microalgues éliminent les métaux lourds: voici comment 🧪
miniature
1
Et voici un qubit mécanique ! 🖥️
miniature
Les lentilles de contact sont-elles vraiment sans danger ? 👁️
miniature
Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥
miniature
4
Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠
miniature
Cette astuce quotidienne ajoute 11 ans à votre vie 🕒
miniature
Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋
miniature
Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀
miniature
Voici pourquoi l'alcool peut rendre agressif 🥂
miniature
Expérience inédite: ce laser projette une ombre visible 💥
Page générée en 0.255 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise