Inégalité d'Azuma - Définition
La liste des auteurs de cet article est disponible ici.
Énoncé général
Un énoncé plus général (McDiarmid, Théorème 6.7) est le suivant
Théorème — Soit une martingale
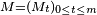
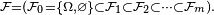
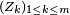
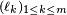
![\scriptstyle\ k\in[\![1,m]\!],\](https://static.techno-science.net/illustration/Definitions/autres/9/9ebddb3c5f87b45cb9775ed517a264d4_8fb2a866937b1483473976034f9a4fdc.png)
-
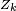
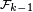
-
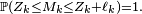
Alors, pour tout 
![\begin{align} \mathbb{P}\left(M_m-\mathbb{E}[M_m]\ge \lambda\right) &\le\exp\left(-\frac{2\lambda^2}{\sum_{i=1}^m\ell_i^2}\right), \\ \mathbb{P}\left(M_m-\mathbb{E}[M_m]\le -\lambda\right) &\le\exp\left(-\frac{2\lambda^2}{\sum_{i=1}^m\ell_i^2}\right), \\ \mathbb{P}\left(\left|M_m-\mathbb{E}[M_m]\right|\ge \lambda\right) &\le 2\exp\left(-\frac{2\lambda^2}{\sum_{i=1}^m\ell_i^2}\right). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/b/bea65989aad4c3b966ce68f81cdcd0fc_9ac1e0bc35efee23174d5cd15843e680.png)
L'énoncé courant, donné à la section précédente, est obtenu en spécialisant l'énoncé général aux choix
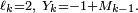
La démonstration est analogue à celle de l'inégalité de Hoeffding : on pose
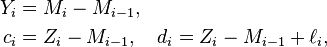
et on remarque que
![\begin{align} \mathbb{P}\left(c_i\le Y_i\le d_i\right)&=1, \\ d_{i}-c_{i}&=\ell_{i}, \\ M_{m}-\mathbb{E}[M_{m}]&=Y_{1}+Y_{2}+\dots+Y_{m}. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/2/20506c6904456a97ce60156e2aee6fc5_497c6fbceb22fec28c5273eb8db8b79a.png)
Pour tout  on a donc, en vertu de l'inégalité de Markov :
on a donc, en vertu de l'inégalité de Markov :
![\begin{align} \mathbb{P}\left(M_{m}-\mathbb{E}[M_{m}]\ge \lambda\right) &\le\mathbb{E}\left[e^{s(M_{m}-\mathbb{E}[M_{m}])}\right]e^{-s\lambda} \\ &=\mathbb{E}\left[e^{s(Y_{1}+Y_{2}+\dots+Y_{m})}\right]e^{-s\lambda} \end{align}](https://static.techno-science.net/illustration/Definitions/autres/c/c84a0ec481fcf2d843881dc3258dfbb3_a0181e3181cf6f1d7cdbc0fad738ab91.png)
On remarque alors que
![\begin{align} \mathbb{E}\left[e^{sY_{m}}\left|\mathcal{F}_{m-1}\right.\right] &\le\exp\left(s^2\ell_m^2/8\right), \end{align}](https://static.techno-science.net/illustration/Definitions/autres/d/d0fbeb725fa0dc49d7883b1fc0ce46e2_af8ce74a4aa41631aaed5af27dadfc64.png)
en vertu de l'inégalité suivante (qui est le premier pas de la démonstration de l'inégalité de Hoeffding) :
Proposition — Soit
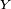
![\scriptstyle\ \mathbb{E}[Y]=0\](https://static.techno-science.net/illustration/Definitions/autres/7/79eafb8ba68d587b62b98e058f29ae22_d65bb214cbd4a2f3efc94a3edc87a58c.png)
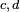
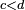
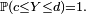

![\mathbb{E}\left[e^{sY}\right]\le\exp\left(s^2(d-c)^2/8\right).](https://static.techno-science.net/illustration/Definitions/autres/6/6960962fffebfd110beeb689d5f15cb1_46efceb40d12a47c8d82da35478dfa6d.png)
En effet
![\begin{align} \mathbb{E}\left[Y_{m}\left|\mathcal{F}_{m-1}\right.\right]&=0, \\ \mathbb{P}\left(c_{m}\le Y_{m}\le c_{m}+\ell_m\left|\mathcal{F}_{m-1}\right.\right)&=1, \end{align}](https://static.techno-science.net/illustration/Definitions/autres/4/4f4fe19eea665a0812beabf61f62c43c_4bd1a01c68b7d09818d4714de82af400.png)
et la variable aléatoire
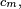
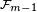
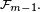
![\begin{align} \mathbb{E}\left[e^{s(Y_{1}+Y_{2}+\dots+Y_{m})}\right] &=\mathbb{E}\left[\mathbb{E}\left[e^{s(Y_{1}+Y_{2}+\dots+Y_{m})}\left|\mathcal{F}_{m-1}\right.\right]\right] \\ &=\mathbb{E}\left[e^{s(Y_{1}+Y_{2}+\dots+Y_{m-1})}\ \mathbb{E}\left[e^{sY_{m}}\left|\mathcal{F}_{m-1}\right.\right]\right] \\ &\le\mathbb{E}\left[e^{s(Y_{1}+Y_{2}+\dots+Y_{m-1})}\right]\ e^{s^2\ell_m^2/8} \\ &\le\exp\left((\sum_{i=1}^m\ell_i^2)s^2/8\right), \end{align}](https://static.techno-science.net/illustration/Definitions/autres/d/d1999cd24aaf86b1c008cc020cccacca_3daafc90ccd4bbc8bef4ff6f0aab0236.png)
la dernière inégalité étant obtenue par récurrence. On obtient ainsi la même inégalité intermédiaire que dans la démonstration de l'inégalité de Hoeffding, et on termine donc la démonstration de la même manière que pour l'inégalité de Hoeffding.

















































