Jeu de la vie - Définition

Introduction

Le jeu de la vie, automate cellulaire imaginé par John Horton Conway en 1970, est probablement, à l’heure actuelle, le plus connu de tous les automates cellulaires.

Malgré des règles très simples, le jeu de la vie permet le développement de motifs extrêmement complexes.

Règles

En préambule, il faut préciser que le jeu de la vie n’est pas vraiment un jeu au sens ludique, puisqu’il ne nécessite aucun joueur ; il s’agit d’un automate cellulaire, un modèle où chaque état conduit mécaniquement à l’état suivant à partir de règles pré-établies.

Le jeu se déroule sur une grille à deux dimensions, théoriquement infinie (mais de longueur et de largeur finies et plus ou moins grandes dans la pratique), dont les cases — qu’on appelle des « cellules », par analogie avec les cellules vivantes — peuvent prendre deux états distincts : « vivantes » ou « mortes ».

À chaque étape, l’évolution d’une cellule est entièrement déterminée par l’état de ses huit voisines de la façon suivante :

• Une cellule morte possédant exactement trois voisines vivantes devient vivante (elle naît).
• Une cellule vivante possédant deux ou trois voisines vivantes le reste, sinon elle meurt.

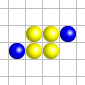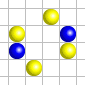
Ainsi, la configuration donne au tour suivant la configuration qui redonne ensuite la première.

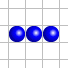
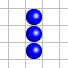
On peut également formuler cette évolution ainsi :

• 
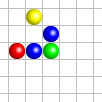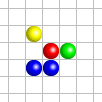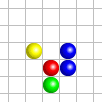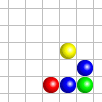
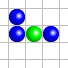
  Si une cellule a exactement trois voisines vivantes, elle est vivante à l’étape suivante. C’est le cas de la cellule verte dans la configuration de gauche.
  
• 
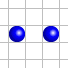
  Si une cellule a exactement deux voisines vivantes, elle reste dans son état actuel à l’étape suivante. Dans le cas de la configuration de gauche, la cellule située entre les deux cellules vivantes reste morte à l’étape suivante.
  
• 
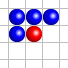
  Si une cellule a strictement moins de deux ou strictement plus de trois voisines vivantes, elle est morte à l’étape suivante. C’est le cas de la cellule rouge dans la configuration de gauche.
  

Légende des schémas

Afin de représenter le processus, les cellules vivantes sont généralement représentées colorées sur la grille, sur un fond de cellules mortes incolores.

Les schémas de cet article suivent les conventions de couleur suivantes :

• bleu : cellules en cours de vie
• vert : cellules naissantes
• rouge : cellules mourantes
• jaune : cellules ne vivant qu’une seule génération

Structures

Des structures, constituées de plusieurs cellules, peuvent apparaître dans l’univers ; les plus classiques sont :

• Les structures stables
• Les structures périodiques, ou oscillateurs
• Les vaisseaux

Il existe également d’autres structures, qui n’apparaîssent pas spontanément dans l’univers de jeu :

• Les puffeurs
• Les canons
• Les jardins d’Éden

Structures stables

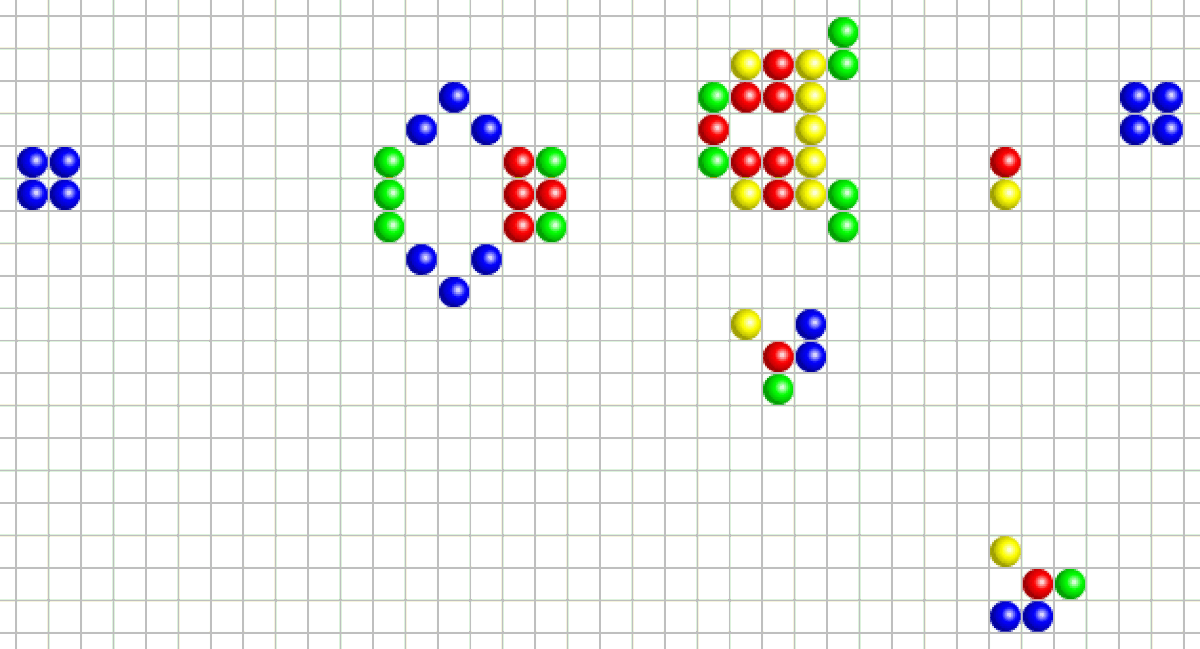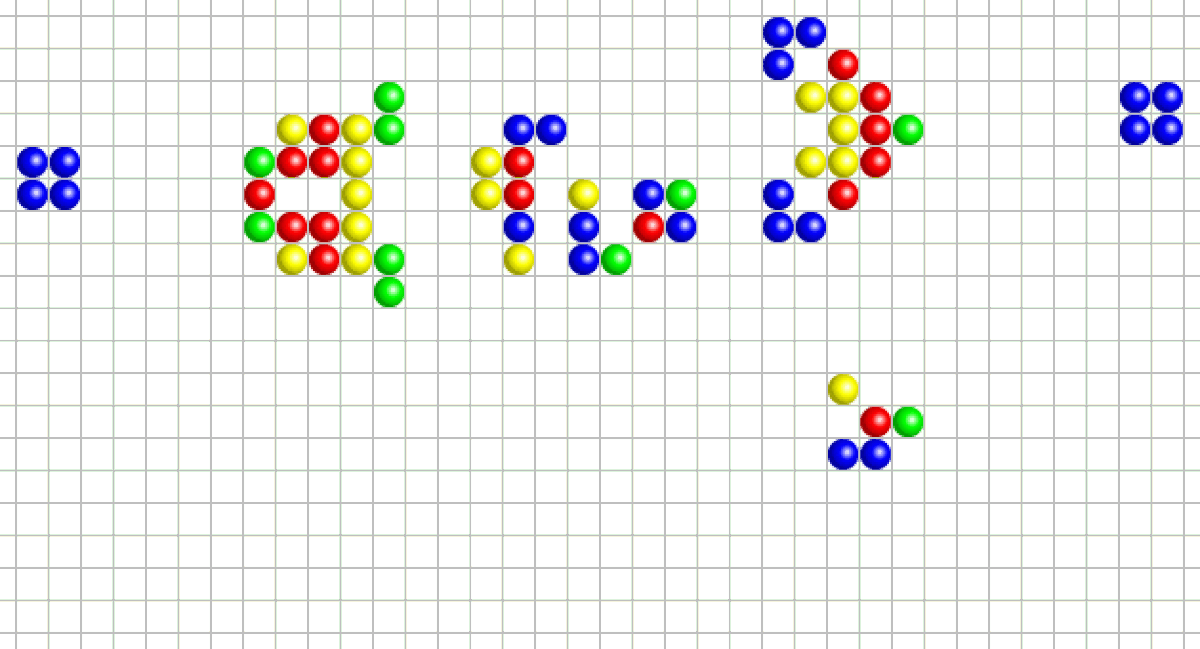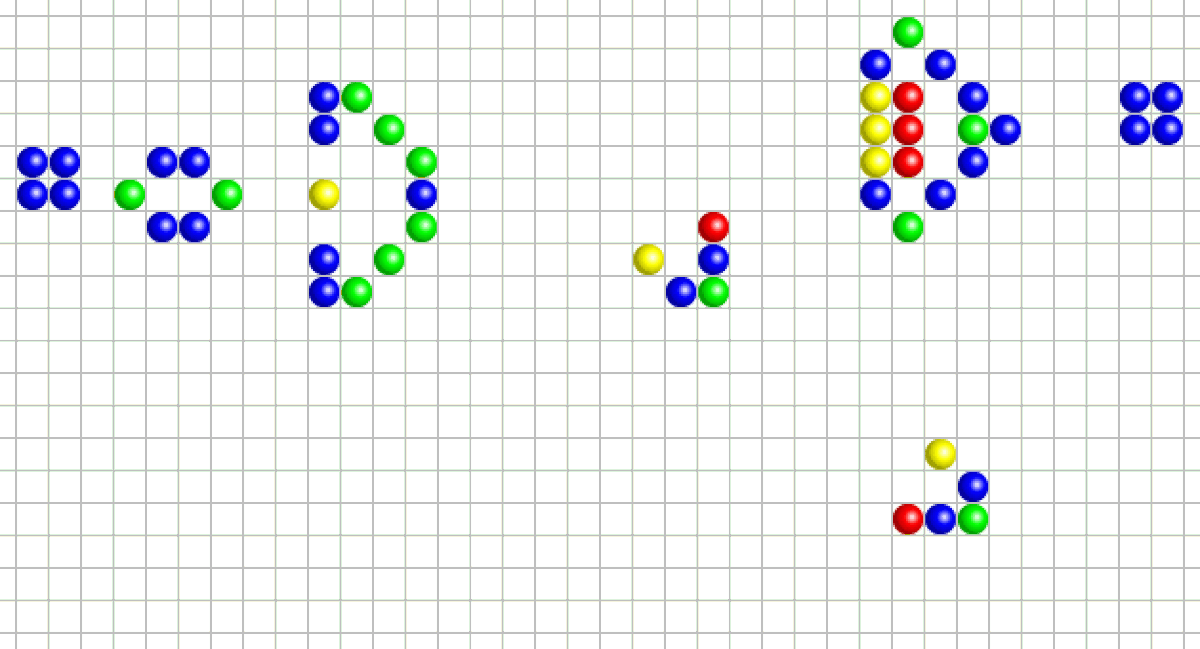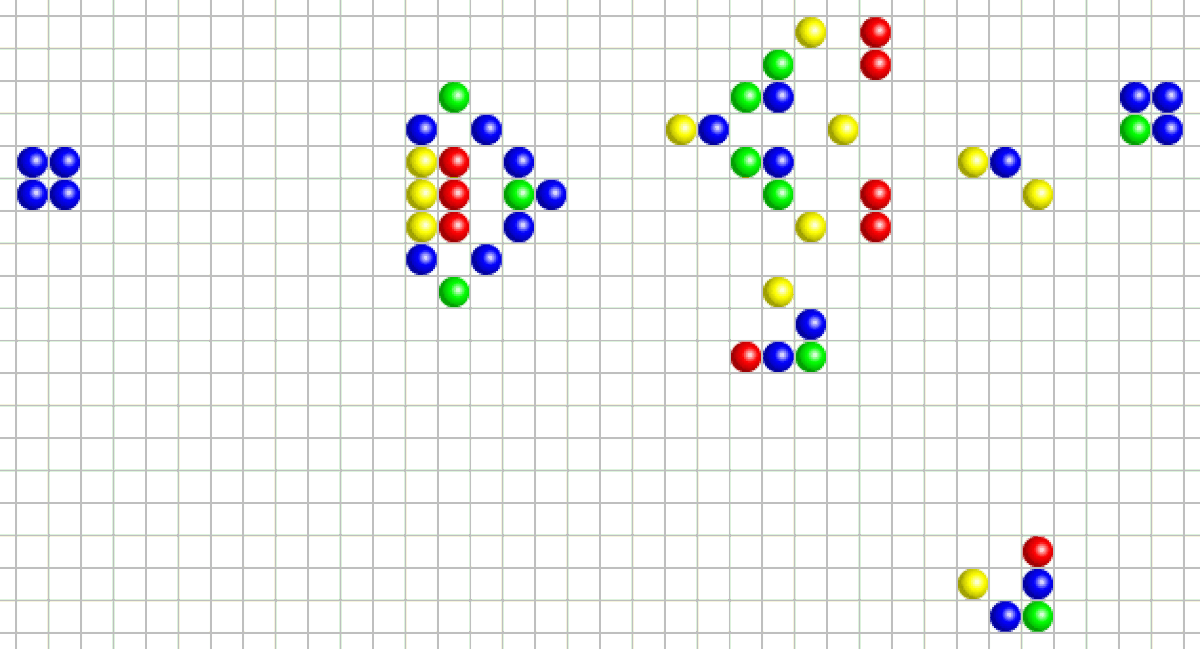
Les structures stables (en anglais still life) sont des ensembles de cellules ayant stoppé toute évolution : elles sont dans un état stationnaire et n’évoluent plus tant qu’aucun élément perturbateur n’apparaît dans leur voisinage. Un bloc de quatre cellules est la plus petite structure stable possible.

Oscillateurs

Les oscillateurs se transforment de manière cyclique, en revêtant plusieurs formes différentes avant de retrouver leur état initial. Des figures de ce type sont très nombreuses : on en connaît actuellement des centaines. La « grenouille » est une structure qui se répète toutes les deux générations.

Elles peuvent apparaître relativement facilement dans l’univers de jeu par l’évolution spontanée de « graines » beaucoup plus simples.

Vaisseaux

Les vaisseaux — ou navires — (en anglais spaceships, « vaisseaux spatiaux ») sont des structures capables, après un certain nombre de générations, de produire une copie d’elles-mêmes, mais décalée dans l’univers du jeu.

Le déplacement d’un vaisseau qui, après n étapes, retrouve sa configuration initiale déplacée de A cases horizontalement et de B cases verticalement est noté A - B. L’existence de vaisseaux de type A - B pour A et B quelconques a été démontrée, mais on ne connaît actuellement que deux grands types de vaisseaux :

• Des vaisseaux de type transversal, c’est-à-dire A = 0 ou B = 0.
• Des vaisseaux de type diagonal, avec A = ± B.

On prouve également qu’un vaisseau de type A - B a nécessairement une période N ≥ 2(A+B).

On sait construire des vaisseaux de taille et de période aussi grandes que souhaitées, en utilisant des séries de composants. Le planeur est le plus petit vaisseau du Jeu de la vie.

Puffeurs

Les puffeurs (de l’anglais puffer, « générateur de fumée ») sont des configurations qui se déplacent en laissant derrière elles une traînée constituée de débris.

Canons

Les canons, ou lanceurs, ou encore lances-navires (en anglais guns) sont capables de produire des vaisseaux, à un rythme variable (toutes les 15, 23, 30 ou 360 générations par exemple, ou bien de manière apparemment imprévisible pour les lance-navires pseudo-aléatoires).

De telles structures peuvent être créées à partir de puffeurs que l’on modifie afin que les débris s’agencent sous forme de navires. Le premier canon à avoir été découvert émet un planeur toutes les 30 générations.

Jardins d’Éden

Un jardin d’Éden est une configuration sans passé possible : aucune configuration ne donne à l’étape suivante un jardin d’Éden.

La démonstration mathématique se fonde sur la combinatoire et se trouve notamment dans Winning Ways for your Mathematical Plays, un livre publié en 1982 par Berlekamp, Conway, et Guy.

Dimension et complexité

Actuellement, la puissance des ordinateurs permet l’exploration de très grands espaces cellulaires du jeu de la vie. On peut alors en espérer l’émergence de structures complexes d’un haut niveau d’auto-organisation, voire d’esthétique. Stephen Wolfram et d’autres ont exploré cette voie. Dès les années 1980, le clown émerge à l’itération 110 d’une dynamique d’un réseau amorcé à partir d’un U initial de 7 cellules formant une image de la lettre U.

NB : Le clown est formé à l’envers… Pour voir un clown comme sur l’illustration, c’est un U inversé qu’il faut dessiner.

Détails sur la dynamique du réseau : ce « U » de 7 cellules évolue vers une structure complexe et « organique » en passant par des formes très esthétiques. De plus, la structure est auto-reproductible avec un déphasage : la nouvelle structure fille (itération 45) interférant avec une version de la structure mère (itération 15) en cours d’évolution. À l’itération 110 on obtient cette belle image de « clown ». Puis le réseau se stabilise sur une forme stable oscillante complexe.