Topologie quotient - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la topologie quotient consiste intuitivement à créer une topologie en collant certains points d'un espace donné sur d'autres, par le biais d'une relation d'équivalence bien choisie. Cela est souvent fait dans le but de construire de nouveaux espaces à partir d'anciens. On parle alors d'espace quotient.
Introduction
Beaucoup d'espaces intéressants, le cercle, les tores, le ruban de Möbius, les espaces projectifs sont définis comme des quotients. La topologie quotient fournit souvent la façon la plus naturelle de munir un ensemble défini "géométriquement" d'une topologie naturelle. Citons par exemple (voir plus bas) l'ensemble des sous-espaces vectoriels de dimension
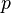
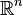
Citons aussi le cas des surfaces de
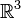
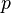
Cette notion illustre aussi l'efficacité de la topologie générale par rapport à la théorie des espaces métriques, souvent utilisée comme introduction à la topologie : bien que la topologie de la plupart des exemples décrits ci-dessous puisse être définie par une métrique, une telle métrique n'est pas toujours facile à construire.
Recollements
Soient
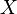
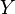
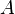
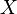
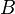
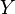

Le recollement de
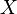
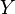


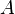
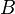

On peut décrire ainsi l'opération consistant à ajouter une anse à une surface
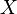
![Y=S^1\times [0,1]\,](https://static.techno-science.net/illustration/Definitions/autres/4/4a58382293c6f77d8ba4cd1fb8ca04db_6fda9d4f96740d0dabc252f6a49920f1.png)







Définition et principales propriétés
Soit
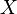
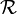
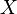
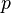
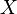

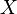
La topologie quotient sur



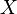
Soit
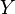


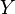

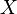
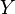
La définition de la topologie quotient est faite précisément pour que cette propriété soit satisfaite : si
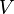



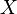

Remarque
Ce critère nous dit aussi que si une application continue
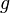
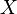
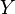


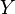
Quelques pièges
Le prix à payer pour la simplicité de cette définition est le fait que même si
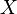

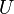
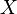


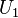
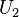
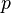
Premiers exemples
- Si
![X=[0,1]\,](https://static.techno-science.net/illustration/Definitions/autres/7/7d71db66a4cafccefd55b0d128b05557_1dcddbfbd81e7d14ab03f3a580a41800.png)
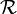
identifie
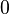
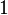

- Si
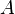
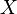
notons

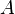
- * Si
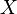
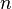
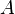
(qui est la sphère unité



- * Si