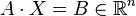Matrice tridiagonale - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, en algèbre linéaire, une matrice tridiagonale est une matrice telle que les coefficients qui ne sont pas sur la diagonale, sur la diagonale juste au-dessous ou sur la diagonale juste au-dessus sont tous nuls.
Par exemple, la matrice suivante est tridiagonale :
Définition
Une matrice
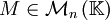
-
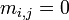
 .
.
Utilisation
Algorithmes
De nombreux algorithmes d'algèbre linéaire nécessitent bien moins d'opérations lorsqu'on les execute sur des matrices diagonales. Il est courant que ce gain se propage aux matrices tridiagonales.
Par exemple, le déterminant d'une matrice tridiagonale A n×n peut être calculé par la formule récursive suivante :
où l'on note le k-ième mineur, c'est-à-dire le déterminant de la matrice obtenue en ne gardant que les k premières lignes et colonnes de A. Le calcul du déterminant par cette méthode est linéaire en n pour les matrices tridiagonales, alors qu'il est en n³ dans le cas général.
Une transformation qui réduit une matrice quelconque à une matrice de Hessenberg réduira une matrice hermitienne à une matrice tridiagonale. Ainsi, de nombreux algorithmes de calcul des valeurs propres utilisent une étape de réduction sous la forme d'une matrice tridiagonale s'ils travaillent sur des matrices hermitiennes.
Mémoire
Une matrice tridiagonale peut être stockée de façon optimisée en utilisant une représentation particulière. Par exemple, la librairie LAPACK enregistre une matrice non-symétrique sous la forme de trois tableaux unidimensionnels, l'un contenant les coefficients diagonaux et les deux autres les éléments respectivement au-dessus et au-dessous de la diagonale.
Mathématiques
Les matrices tridiagonales sont courantes dans l'étude des splines cubiques. Elles sont également souvent des solutions au problème de Sturm-Liouville.
D'autre part, un système linéaire implicant une matrice tridiagonale, de la forme :
peut être résolu au travers d'algorithmes spécifiques, qui nécessitent O(n) opérations (Golub et Van Loan).
Propriétés
Une matrice tridiagonale est une matrice de Hessenberg.
Si une matrice réelle tridiagonale A vérifie ak,k+1 × ak+1,k > 0 pour k = 1, 2, ..., n — c’est-à-dire que les signes de ces coefficients sont symétriques, alors elle est semblable à une matrice hermitienne, et donc toutes ses valeurs propres sont réelles. Cette dernière propriété est conservée si on considère plutôt la condition ak,k+1 × ak+1,k ≥ 0.
L'ensemble de toutes les matrices tridiagonales n × n est un espace vectoriel de dimension 3n-2.
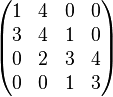
![\det A = a_{n,n} \det \, [A]_{\{1,\ldots,n-1\}} - a_{n,n-1} a_{n-1,n} \det \, [A]_{\{1,\ldots,n-2\}} \, ,\,](https://static.techno-science.net/illustration/Definitions/autres/6/611c954597fa4043dfc1e98113b9cd4f_84baf4377856b4213d47d66e7a477dc0.png)