Mécanique des milieux continus - Définition
La liste des auteurs de cet article est disponible ici.
Approche simplifiée : contrainte, déformation et coefficients élastiques
La base de la mécanique des milieux continus est l'étude des déformations et des phénomènes associés à une transformation d'un milieu. La notion de déformation sert à quantifier de quelle manière les longueurs ont été dilatées et les angles ont changé dans le milieu.
Une manière simple pour chercher à quantifier la déformation, est de regarder l'allongement relatif d'un segment dans le solide, ou la variation d'angle entre deux directions.
Pour l'allongement relatif ε, encore appelé déformation
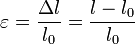
l0 étant la longueur initiale et Δl l'allongement ; ε est sans unité.
On pourra remarquer que lors d'une sollicitation en traction, ε est positif, et que lors d'une compression, il est négatif.
Cette notion introduite ici est « globale » en cela que l'on regarde l'allongement relatif pour un segment de longueur l0.
Pour introduire une notion locale, il faut considérer la limite de l'allongement relatif lorsque la longueur du segment tend vers 0 :
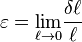
On se rend alors compte que la notion d'allongement relatif est assez pauvre, car au cœur du volume d'un solide, on peut considérer une infinité de direction pour les segments. Cette notion est cependant suffisante pour appréhender l'étude des poutres.
Les sollicitations sont quantifiées par la notion de contrainte σ, qui est l'effort surfacique exercé sur une partie de la pièce en un point par le reste de la pièce.
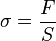
σ est homogène à une pression et est exprimé en mégapascal (MPa) ou en Newton par millimètre carré (N/mm²).
Le fait d'utiliser σ et ε permet d'écrire des lois locales et non globales, on peut alors écrire l'équilibre de chaque point du milieu et décrire son comportement (loi liant la contrainte et la déformation).
Le matériau est caractérisé par des coefficients élastiques, qui représentent la difficulté à déformer ; le principal est le module d'Young E, relié à la contrainte et la déformation par la loi de Hooke :
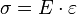
E est homogène à une pression et est exprimé en gigapascal (GPa) ou en Newton par millimètre carré (N/mm²).
Cinématique des milieux continus (description lagrangienne)
On décrit la transformation de chaque point du milieu par une fonction (suffisamment régulière)
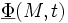
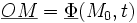
On introduit alors le concept de déformation, pour mesurer la variation de distance entre deux points du solide suite à la transformation
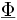
On cherche à avoir une mesure de
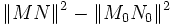
Or on a
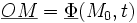
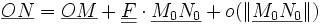
Où
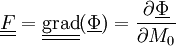
est le gradient de la transformation.
On obtient donc :
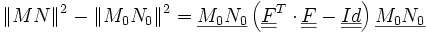
On pose :
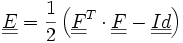
où
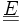
Si on introduit le vecteur déplacement
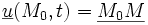
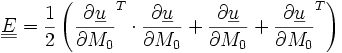
Si l'on fait l'hypothèse des petites déformations, on obtient l'opérateur des déformations linéarisé :
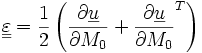
Essais mécaniques simples
Ces essais permettent de mesurer, pour un objet, les principales grandeurs caractéristiques liées à la matière dont il est constitué.
Lois empiriques de comportement
Les lois empiriques de comportement sont des lois dérivées des observations et de l'expérience, qui décrivent les déformations ou les contraintes en fonction des sollicitations (vitesse de déformation, température...).
Tenseur des contraintes
Dans le cas général, un élément de matière situé au cœur d'une pièce est soumis à des contraintes dans diverses directions. Dans le cadre de la théorie du premier gradient, on représente cet état de contrainte par un tenseur d'ordre deux (que l'on peut lui même représenter par une matrice 3×3) appelé tenseur des contraintes.

















































