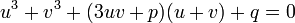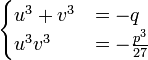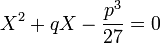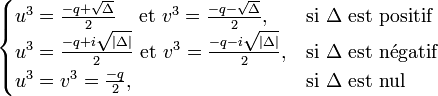Méthode de Cardan - Définition

Principe de la méthode

Considérons l'équation générale du troisième degré suivante : .

En posant , on se ramène à une équation de la forme :
où et .

On va maintenant poser avec u et v complexes, de façon à avoir deux inconnues au lieu d'une et se donner ainsi la possibilité de poser ultérieurement une condition sur u et v permettant de simplifier le problème. L'équation devient ainsi

.

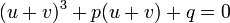
Cette équation se transforme aisément sous la forme suivante :

La condition de simplification annoncée sera alors . Ce qui nous donne d'une part et d'autre part , qui, en élevant les deux membres à la puissance 3 donne .

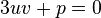
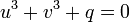
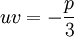
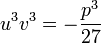
Nous obtenons finalement le système somme-produit des deux inconnues u³ et v³ suivant :

Les inconnues u³ et v³ étant deux complexes dont on connaît la somme et le produit, ils sont donc les solutions de l'équation du second degré :

Le discriminant de cette équation est et les racines sont

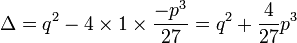
Il suffit alors d'associer les trois racines cubiques de u³ et v³ deux par deux de façon à obtenir trois couples (u,v) tel que , puis reporter les trois couples de valeurs trouvés pour u et v dans l'expression .

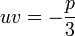
Enfin, on revient au premier changement de variable pour avoir les trois racines de l'équation du troisième degré posée au départ.

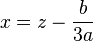
Remarque historique

Une polémique concernant la paternité de cette méthode existe.

On raconte que la méthode fut précédemment découverte par le mathématicien italien Tartaglia. À cette époque, les mathématiciens se lançaient des défis pour résoudre des équations du troisième degré et Tartaglia les résolvait toutes. Intrigué, Cardan lui a demandé s'il n'aurait pas trouvé des méthodes. Après s'être fait prier et avoir reçu l'assurance que Cardan ne les dévoilerait à personne, Tartaglia les lui confia. Quelle ne fut pas sa surprise de voir Cardan les publier en 1545.

On appelle désormais souvent ces formules les formules de Tartaglia-Cardan.

L'utilisation des formules de Cardan nécessite parfois l'utilisation de nombres complexes, même pour trouver des solutions réelles. En fait, les nombres imaginaires sont précisément nés à cette occasion.

Dans l'exemple z³ = 15z + 4 ou bien z³ - 15z - 4 = 0, on a p = - 15 et q = -4, donc : et u³ + v³ = 4 donc u³ et v³ sont racines de l'équation X² - 4X + 125 = 0, dont les racines n'existent pas. Pourtant, il y a bien une solution z à l'équation initiale ; c'est z = 4. C'est Bombelli qui surmontera cette difficulté en proposant pour la première fois un calcul sur les nombres imaginaires. La résolution formelle de l'équation X² - 4X + 125 = 0 donne pour racines et , or Bombelli s'aperçoit que le cube de vaut et que le cube de vaut . Il en déduit que et que et il trouve bien finalement comme solution z = u + v = 4.

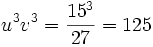
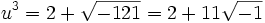
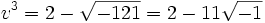
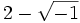
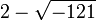
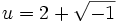
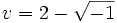
Les nombres imaginaires sont nés.