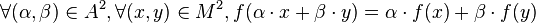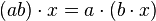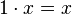Module sur un anneau - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un module sur un anneau unitaire est une structure algébrique qui généralise celle d'espace vectoriel et celle d'idéal d'un anneau.
Dans un espace vectoriel l'ensemble des scalaires forme un corps tandis que dans un module, ceux-ci sont de manière plus générale munis d'une structure d'anneau (non nécessairement commutatif). Une partie des travaux en théorie des modules consiste à retrouver les résultats spectaculaires de la théorie des espaces vectoriels, quitte pour cela à travailler avec des anneaux plus maniables, comme les anneaux principaux.
Comparaison avec la structure d'espace vectoriel
Certaines propriétés vraies pour les espaces vectoriels ne sont plus vraies pour les modules. Par exemple l'existence d'une base n'y est plus assurée, et on ne peut pas nécessairement y développer de théorie de la dimension, même dans un module engendré par un nombre fini d'éléments.
Les modules ne sont pas une généralisation inutile. Ils apparaissent naturellement dans beaucoup de situations algébriques ou géométriques. Un exemple simple est un module sur l'anneau des fonctions infiniment différentiables sur un ouvert : il est naturel de ne pas pouvoir y faire de division, puisqu'il vaut mieux éviter de diviser par 0. De la même façon, il est naturel de considérer un module sur l'anneau des polynômes à une ou plusieurs variables.
Applications linéaires
Une application linéaire f entre deux modules M et N sur un même anneau A est une fonction qui conserve la structure de module, i.e qui vérifie :
Autrement dit, une application linéaire est un morphisme de modules. Si f est bijective, on dit de plus que f est un isomorphisme. Si les modules de départ et d'arrivée M et N sont identiques, on dit que f est un endomorphisme. Si f est à la fois un endomorphisme et un isomorphisme, on dit que c'est un automorphisme.
Le noyau d'une application linéaire f est l'ensemble des éléments x de M qui vérifient f(x) = 0. C'est un sous-module de M et il est noté Ker f. On peut également définir l'image d'une application linéaire Im f = f(M) qui est un sous-module de N.
Comme dans le cas des groupes ou des anneaux, un morphisme de A-modules 
donne lieu à un isomorphisme 
, défini par 
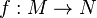
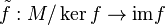
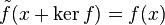
Définitions
Module à gauche, module à droite
Si A est un anneau (unitaire), et (M , +) un groupe commutatif.
Si de plus, M est muni d'une loi externe 
de A × M dans M vérifiant, pour tous éléments a et b de A et x, y de M :
(distributivité de par rapport à l'addition dans M)
(distributivité de par rapport à l'addition dans A)
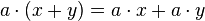
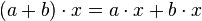
- Remarque : la loi + du membre de gauche est celle de l'anneau A et la loi + du membre de droite est celle du groupe M
alors (M, + , ) est un A-module à gauche.
Ce qui a été défini ici est un A-module à gauche, car, dans la loi externe, les éléments de A sont placés à gauche. On pourra définir de même un A-module à droite.
Il est important de remarquer que les structures de module à gauche et à droite ne diffèrent pas uniquement par leur écriture : si les deux premiers axiomes sont les mêmes, le troisième s'écrit 
. Si l'on transcrivait naïvement cette égalité en écrivant les éléments de A gauche, on obtiendrait 
, ce qui, si A n'est pas commutatif, ne revient pas au même que l'axiome qui donne la structure de module à gauche.
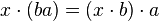
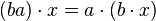
Par contre, le petit raisonnement ci-dessus montre que, si l'on "inverse" la loi de A, un module à droite peut être vu comme un module à gauche. Plus précisément, notons Aop l'anneau "opposé" à A, c'est-à-dire le groupe abélien A muni de la multiplication définie par aopbop = ba, si aop et bop désignent a et b vus comme éléments de Aop. Alors, si M est un A-module à gauche, M peut être vu comme un Aop-module à droite, où l'action de Aop est définie par a.m = m.aop.
Ceci justifie que dans la suite, on puisse se restreindre à l'étude des modules à gauche.
Exemples
- Lorsque A est un corps, on retrouve la structure habituelle de A-espace vectoriel. Dans ce cas, les éléments de A sont appelés les scalaires, les éléments de M sont appelés les vecteurs.
- A lui-même est à la fois un module à gauche et à droite.
- L'ensemble des vecteurs du plan dont les coordonnées sont des entiers relatifs forme un
-module. - Tout groupe abélien est automatiquement un -module pour la loi externe définie par :
-
- pour n > 0,
avec n termes x - pour n = 0
- pour n < 0,
avec |n| termes x
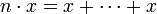
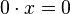
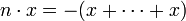
- pour n > 0,
Cette loi est la seule qui munisse un groupe abélien d'une structure de -module. Il y a donc équivalence entre la notion de -module et celle de groupe abélien.
- La structure de A-module apparaît dans celle d'algèbre sur un anneau.
- Si M un groupe abélien et si f est un endomorphisme de groupe sur M, alors on peut définir la loi externe
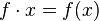
qui confère à M une structure de End(M)-module . - Si M est un espace vectoriel, on peut faire la même chose avec des endomorphismes d'espaces vectoriels au lieu de groupes. Par exemple, l'espace vectoriel
à n dimensions est un module à gauche sur 
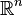
via la multiplication matricielle. - Si M est un A-module à gauche, l'ensemble des applications d'un ensemble S vers M est un A-module à gauche, pour les lois (f + g)(x) = f(x) + g(x) et
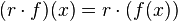
- Un espace vectoriel
sur un corps 
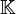
peut être considéré comme un module sur l'anneau principal ![\mathbb K[X]](https://static.techno-science.net/illustration/Definitions/autres/1/11cf18672fa8c102e5d2ec8bdfe203c8_bd379140d6a603f16bfb95868779a783.png)
, et par ce biais la majeure partie des propriétés de l'algèbre linéaire peut être démontrée.
Cette structure de module est la suivante : étant donné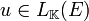
fixé, pour tout ![\left( p, x \right) \in \mathbb K[X]\times E](https://static.techno-science.net/illustration/Definitions/autres/4/4fe3999552e4b77d3dcb48d887246383_b92cd15b4ecbbad140a9c0b97692ad90.png)
, on pose 
, avec 
car cet ensemble a une structure d'algèbre sur .
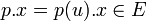
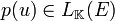
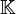
Lien avec la théorie des représentations
Le premier axiome montre que, pour 
, l'application 
est un endomorphisme du groupe M. Les trois axiomes suivants traduisent quant à eux le fait que l'application 
est un morphisme (unitaire) de l'anneau A dans l'anneau des endomorphismes de M, noté End(M).
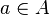
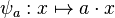
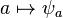
Réciproquement, la donnée d'un morphisme d'anneau unitaire 
fournit à M une structure de A-module (à gauche) via la loi 
. Une structure de A-module est donc équivalente à la donnée d'un morphisme 
.
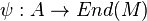
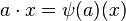
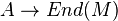
Un tel morphisme A 
End(M) est appelé une représentation de A sur le groupe abélien M. Une représentation est dite fidèle si elle est injective. En termes de module, cela signifie que si pour tout 
, alors a = 0.
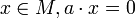
Ceci est une généralisation de ce que l'on trouve en représentation des groupes, où l'on définit une représentation d'un groupe G vers un espace vectoriel sur un corps K comme un morphisme de l'algèbre du groupe K[G] vers End(V), autrement dit, où l'on donne une structure de K[G]-module à V.
Sous-module
Soit E un A-module à gauche, et M une partie de E. On dit que M est un sous-module (à gauche) si les conditions suivantes sont respectées :
- M est un sous-groupe de (E,+)
- Pour tout
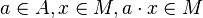
Autrement dit, un sous-module est une partie linéairement stable.
Exemples
- Un cas très important est celui des sous-modules de A en tant A-module : ils ne sont autres que les idéaux à gauche ou à droite selon le type de module choisi, de l'anneau A.
- Si le module est un espace vectoriel, on parle de sous-espace vectoriel
- Dans un groupe commutatif, considéré comme module sur , tout sous-groupe est aussi un sous-module.