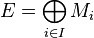Module sur un anneau - Définition

Familles libres, bases

On dit qu'un A-module est de type fini s'il est engendré sur A par un nombre fini d'éléments. On a alors .

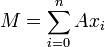
On dit qu'un A-module est libre s'il possède une base sur A (voir module libre).

Si M est de type fini et libre, il existe alors un isomorphisme entre M et Aⁿ, où n est le cardinal de la base.

Opérations sur les modules

Produits de modules

Si on considère une famille de module ( sur un même anneau A, on peut munir l'ensemble produit d'une structure de module en définissant les lois suivantes :

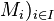
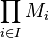
• Loi interne :
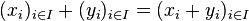
• Loi externe :

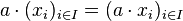
Le module ainsi défini s'appelle le module produit. Les projections sont alors des applications linéaires surjectives. Un exemple important de produit de modules est celui où tous les modules facteurs sont identiques à un même module M ; leur produit M^I n'est alors autre que l'ensemble des applications de I dans M.

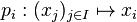
Somme directe de modules

Soit une famille de A-modules, on note leur produit . L'ensemble E des éléments de M dont toutes les composantes sauf un nombre fini sont nulles est appelé somme directe externe de la famille de modules et il est noté :

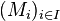
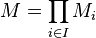
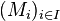
C'est un sous-module de . Dans le cas où I est fini, la somme directe E et le produit M sont évidemment confondus.

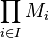
Intersection et somme de sous-modules

Si M est un module, et est une collection de sous-modules de M, on dit que la famille est en somme directe si :

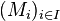
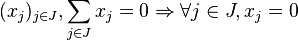
Pour toute partie J finie de I, pour tout

Dans ce cas, la somme , appelée somme directe interne, est isomorphe à la somme directe externe et elle est également notée .

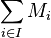
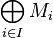
Applications des modules

Les modules sont un outil indispensable pour passer de propriétés géométriques à des propriétés fonctionnelles, ou ressemblant à des propriétés fonctionnelles. Ainsi, au lieu de voir une variété différentiable comme une partie d'un espace concret ou abstrait, on va plutôt considérer une classe de fonctions sur cette variété et déclarer que cette classe est la classe des fonctions différentiables sur la variété -- il faudra satisfaire des conditions appropriées de compatibilité. On pourra ainsi traduire les propriétés géométriques de la variété par des propriétés algébriques de la classe de fonctions que nous avons déclarées comme fonctions différentiables.

Mieux que des fonctions, on peut considérer des champs sur une variété différentiable. Le cas le plus simple est celui des champs tangents différentiables à une variété. Pensons par exemple aux champs de vecteurs tangents à la sphère unité dans un espace de dimension 3. Il s'agit bien d'un module sur l'anneau des fonctions différentiables sur la sphère : si on multiplie un champ différentiable tangent à la sphère par une fonction différentiable, on trouve bien un champ différentiable. Ce module est engendré par la restriction à la sphère des projections tangentes des champs constants égaux aux vecteurs de base de l'espace - cela nous fait trois champs. Mais on peut montrer que ces trois champs ne sont pas indépendants, et on peut même montrer qu'il n'existe aucun choix de deux champs tangents qui pourraient engendrer le module des champs tangents à la sphère et différentiables. On a là l'exemple le plus simple d'un module de type fini, c'est-à-dire engendré par un nombre fini de ses éléments, mais qui ne possède pas de base.

La correspondance systématique entre objet géométrique et objet de nature fonctionnelle est dominante en géométrie algébrique. En effet, si V est l'ensemble des solutions communes d'un système d'équations polynomiales en n variables, on peut étudier l'ensemble des polynômes qui s'annulent sur V; ce sera un idéal de l'anneau des polynômes à n variables, et donc en particulier, un module sur cet anneau. Il est possible de retrouver nombre de propriétés géométrique de V en étudiant les propriétés de cet idéal: points singuliers, dimension, recherche de droites incluses dans V, et ainsi de suite.

Cette faculté d'exprimer les propriétés d'objets géométriques au moyen d'espaces de fonctions sur ces objets est à la base de la géométrie non commutative: les espaces de fonctions sur des objets géométriques usuels sont des anneaux commutatifs pour la multiplication (et même souvent des algèbres, c'est-à-dire des anneaux munis également d'une structure compatible d'espace vectoriel). La démarche de la géométrie non commutative consiste à explorer ce que seraient des objets géométriques sur lesquels vivraient des "fonctions" formant un anneau ou une algèbre non commutative, et c'est pour cette raison que le cas des anneaux non commutatifs et des modules sur des anneaux non commutatifs est très important actuellement.