Moment de force (mécanique) - Définition

En dynamique

En mécanique dynamique, on peut montrer que le moment des forces est la dérivée du moment cinétique par rapport au temps :

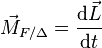
Ceci est l'équivalent du principe fondamental de la dynamique (deuxième loi de Newton) en rotation.

On peut aussi montrer que si est le vecteur vitesse angulaire, c'est-à-dire le vecteur

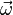
• colinéaire à l'axe de rotation Δ,
• dont la norme est la vitesse angulaire
• et orienté de façon que l'orientation positive d'un plan normal correspond au sens de rotation, alors :

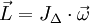
où J_Δ est le moment d'inertie du solide par rapport à l'axe de rotation Δ.