Observable - Définition
La liste des auteurs de cet article est disponible ici.
Observables non normalisables : utilisation de projecteurs
Dans le cas où les vecteurs propres de l'opérateur ne sont pas normalisables, il est indispensable, pour pouvoir calculer des probabilités utilisables, d'employer un autre type d'observable : des projecteurs.
L'observable

-
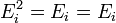
- E1 + E2 + .. + En = I, I étant l'opérateur identité sur

- EiEj = 0 si i ≠ j (projecteurs orthogonaux)
Cet ensemble de projecteur est appelé ensemble complet de projecteurs orthogonaux. On a alors :
L'opérateur est alors dégénéré, dans le sens où les espaces propres (sous-espace vectoriel correspondants à une valeur propre donnée) des projecteurs possèdent plus d'une dimension.
Le cas typique et très utilisé d'opérateur dégénéré utilisant les projecteurs est la question OUI/NON où n=2, et où les valeurs propres de l'opérateur sont fixées à 1 pour "OUI" et 0 pour "NON". Cette observable est alors défini par un seul projecteur E, et tout état quantique
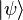
-
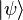
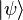
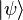
Par exemple, pour l'observable "position", on peut calculer un opérateur dont la valeur propre est 1 si la position est dans un certaine zone, et 0 sinon.
Le cinquième postulat ne s'applique pas à un opérateur dégénéré. Il est remplacé dans ce cas par le postulat de projection, voisin, qui stipule que :
- Si le résultat d'une mesure d'un état quantique
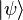
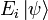
- La probabilité d'obtenir la valeur propre ai est
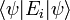
Observables complémentaires
Une paire d'observables est dite complémentaire ou incompatible si son commutateur est non-nul. Selon le principe d'incertitude de Heisenberg, il est impossible de mesurer ou de préciser les valeurs des deux observables simultanément. L'exemple le mieux connu est la position et le moment linéaire (ou impulsion) d'une particule.

















































